14Teoriya változás a lendület és az impulzusmomentum
Mivel a szóban forgó rendszer a tétel lehet bármilyen mechanikus rendszer, amely bármely szervvel.
Az összeg a mozgás (lendület) a mechanikai rendszer említett érték összegével egyenlő a mozgás mennyiségét (impulzus) a valamennyi szerv a rendszerben. A lendület a külső erők a testre ható rendszer - az összege momentumát az összes külső erők a testre ható rendszert.
Tétel a változás a mozgás mértéke követelések
Mennyiségének változtatásával a rendszer mozgását egy ideig egyenlő a lendület a külső erők hatnak a rendszer, hogy ugyanezen időszak alatt.
A törvény megőrzése a rendszer mozgását
Ha az összeg az összes külső erők hatnak a rendszer nulla, akkor a mozgás mértéke (lendület) a rendszer állandó.
Bemutatjuk a változás a lendület a külső erők, megkapjuk kifejeződése tétel a változó száma formájában eltérés a rendszer mozgását:
Így minden az utolsó egyenletet kapjuk javasolja: változás a mozgás mértékét a rendszer valósul meg, csak a keresetet a külső erők és belső erők nincsenek hatással az értékét nem tehetik.
Integrálása mindkét oldalán az egyenlet képest egy tetszőlegesen kiválasztott időintervallum között némi és szerezzen egy kifejezés, a tétel a változó számát a rendszer mozgást szerves formában:
ahol az értékek u a mozgás mennyisége pillanatok vremeniisootvetstvenno, a- impulzus a külső erők azon időtartam alatt. Ennek megfelelően, és a korábban már bevezetett jelölést végeztünk
A törvény lendületmegmaradás (a törvény lendületmegmaradás) bekezdése kimondja, hogy a vektor summaimpulsovvseh telefon rendszer állandó, ha a vektor összege ható külső erők a rendszer nulla.
(Perdület kg · m 2 · s -1)
Tétel változásának perdület középpontjához képest
az idő szerinti deriváltja a perdület (perdület) vonatkozó anyagi szempontból rögzített középpont egyenlő ható erők a pontot képest ugyanabban a központban.
Tétel változásának perdület tengelyhez képest
az idő szerinti deriváltja a perdület (szögsebesség) olyan anyagból pont tekintetében néhány rögzített tengely egyenlő a pillanatban ható ezen a ponton az erő körülbelül ugyanazon a tengelyen.
Tekintsük az anyag M pont massoym. mozgó az intézkedés alapján silyF (3.1 ábra). Mi írjuk a vektor konstrukció és a perdület (perdület) M0 anyagi pont relatív tsentraO:
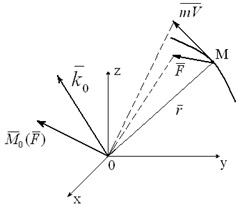
Differenciálás perdület (impulzusmomentum k0) Időpont:
(3.4) képlet fejezi ki a tétel a változás perdület (szögsebesség) egy anyagi pont középpontjához képest: az idő-származékot a perdület (szögsebesség) egy anyagi pont képest néhány fix középső egyenlő a pillanatban ható szorítóerő támadási pontjába viszonyítva ugyanabban a központban.
Kivetítése a (3.4) képlet a tengelye a Descartes-féle koordináták, megkapjuk
Egyenletek (3.5) expresszálják a tétel változásának perdület (szögsebesség) egy anyagi pont tengelyéhez képest: idő szerinti deriváltja a perdület (szögsebesség) olyan anyagból pont tekintetében néhány rögzített tengely egyenlő a pillanatban ható ezen a ponton az erő körülbelül azonos tengely .
Úgy véljük, milyen következményekkel jár a tételek (3.4) és (3.5).
Következmény 1. Vegyük azt az esetet, amikor silaF egész mozgás átmegy a fix pont tsentrO (esetében központi erő), azaz kogdaM0 (F) = 0. Ekkor Tétel (3.4) chtok0 = const,
azaz abban az esetben, központi erő perdület (perdület) az anyag relatív a középpont ezen erő állandó marad nagysága és iránya (3.2 ábra).
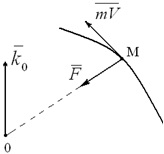
A feltétel k0 = const magában foglalja, hogy a pályáját a mozgó pont egy sík görbe, melynek sík közepén halad át az, hogy erő.
azaz ha a pillanatban ható erő a lényeg képest rögzített tengely mindig nulla, a perdület (impulzusmomentum) attól a ponttól képest ez a tengely állandó marad.
Tétel bizonyítása Ob ihmenenii lendület
Hagyja, hogy a rendszer áll az anyagi tocheks Massamá gyorsulásokat. Minden ható erők a test rendszer, két csoportba sorolhatjuk:
Külső erők - ható erők részéről kívüli szervek vizsgált rendszer. A kapott a ható külső erők egy anyagi pont számot i jelöli.
Belső erők - erők, amelyek kölcsönhatásba lépnek egymással a rendszer szervezetben. Az az erő, amellyel a pontot az i index működik nomeromk ponttal. Jelöljük, és arra kényszeríti vozdeystviyai ponthoz: NAK ponthoz: -. Nyilvánvaló, hogy ha, akkor
A jelöléseket lépett, írja Newton második törvénye az egyes lényeges pontokon tekinthetők
Tekintettel arra, hogy az összes, és összeadjuk az egyenleteket Newton második törvényét, megkapjuk:
A kifejezés az összessége a belső erők hatnak a rendszer. Szerint a Newton harmadik összegben minden silesootvetstvuet silatakaya, chtoi, majd vypolnyaetsyaPoskolku teljes összeg áll az ilyen párok, és az összeg önmagában nulla. Így felírhatjuk
A rendszer a mozgás mértékét jelölés, megkapjuk
Bemutatjuk a változás a lendület a külső erők, megkapjuk kifejeződése tétel a változó száma formájában eltérés a rendszer mozgását:
Így minden az utolsó egyenletet kapjuk javasolja: változás a mozgás mértékét a rendszer valósul meg, csak a keresetet a külső erők és belső erők nincsenek hatással az értékét nem tehetik.
Integrálása mindkét oldalán az egyenlet képest egy tetszőlegesen kiválasztott időintervallum között némi és szerezzen egy kifejezés, a tétel a változó számát a rendszer mozgást szerves formában:
ahol az értékek u a mozgás mennyisége pillanatok vremeniisootvetstvenno, a- impulzus a külső erők azon időtartam alatt. Ennek megfelelően, és a korábban már bevezetett jelölést végeztünk