02 Lineáris függés és függetlenség vektorok
Meghatározások lineárisan függő és független rendszerek vektorok
Tegyük fel, hogy egy olyan rendszer n-vektor
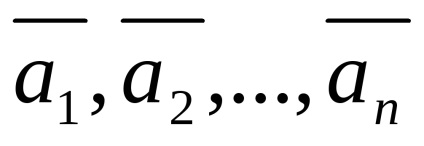
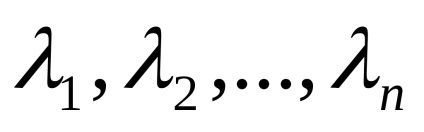
Ez az úgynevezett lineáris kombinációja vektorok az adott rendszer egy adott sor együtthatók.
Definíció 23 (a nulla lineáris kombináció)
vektor rendszer
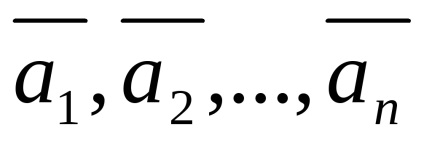
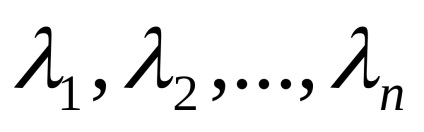
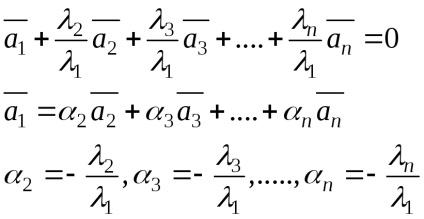
Definíció 24 (vektor útján ábrázolása a rendszer, mint egy lineáris kombinációja a többiek)
vektor rendszer
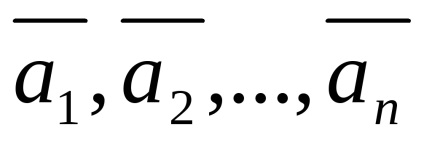
Meghatározások 23. és 24. egyenértékűek.
Definíció 25 (a nulla lineáris kombináció)
vektor rendszer
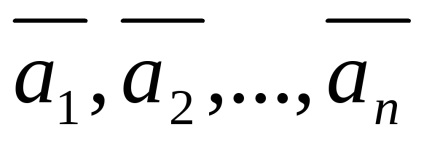
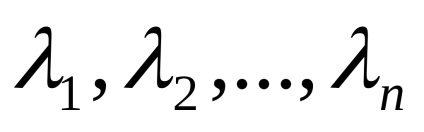
Definíció 26 (via vektor reprezentációi a képtelenség a rendszer, mint egy lineáris kombinációja a többiek)
vektor rendszer
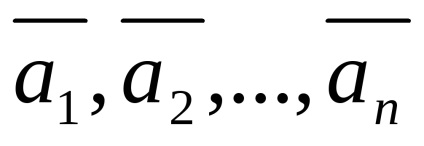
Tulajdonságok lineárisan függő és független rendszerek vektorok
2. Tétel (nulla vektor a vektor rendszer)
Ha a vektor rendszer egy nulla vektor, a rendszer lineárisan függ.
Kapunk tehát lineárisan függ a meghatározását vektorok révén lineáris kombinációja egy nulla (12), a rendszer lineárisan zavisima.
Teorema3 (függő alrendszer vektor rendszer)
Ha a rendszer a vektorok egy lineáris függvény alrendszer, az egész rendszer lineárisan függ.
Legyen
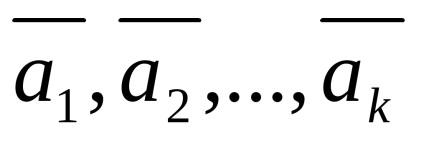
Tehát definíció szerint 23, a rendszer lineárisan függ.
Bármilyen alrendszer lineárisan független rendszer lineárisan független.
Épp ellenkezőleg. Hagyja, hogy a rendszer lineárisan független, és van egy lineáris összefüggés alrendszer. De aztán, a 3. tétel, az egész rendszer is lineárisan függ. Ellentmondás. Következésképpen a lineárisan független alrendszer rendszer nem lehet lineárisan zavisimoy.
A geometriai jelentése lineáris függés és függetlenség vektorok
két vektor

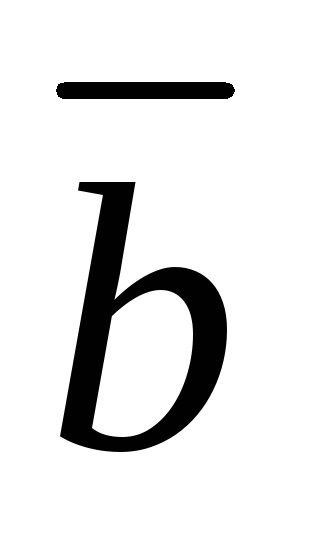
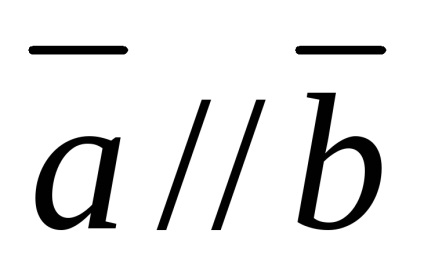

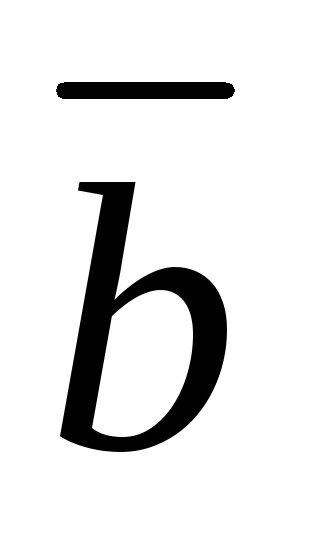
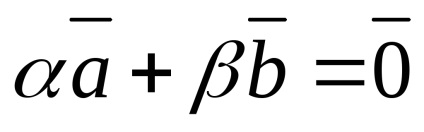
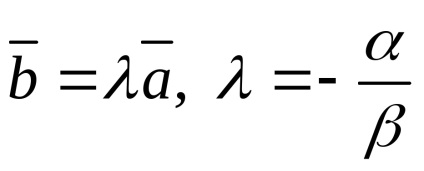
A nulla vektor kollineáris bármely vektorba
Két vektor lineárisan független, ha és csak akkor, ha
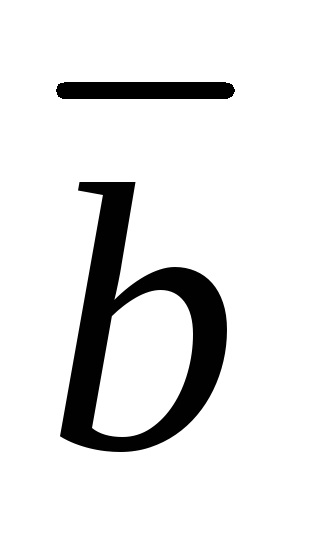

A rendszer a három vektor lineárisan függ akkor és csak akkor, ha ezek a vektorok egy síkban vannak.
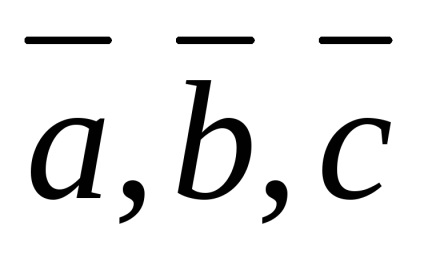
ahol
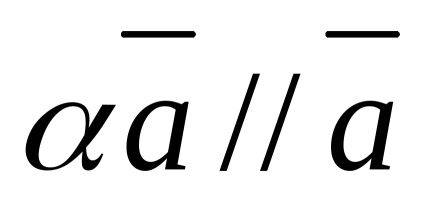
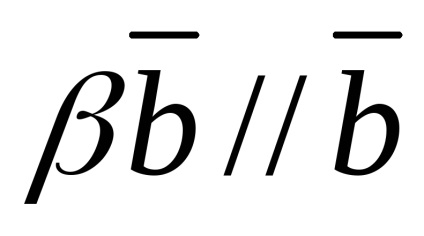
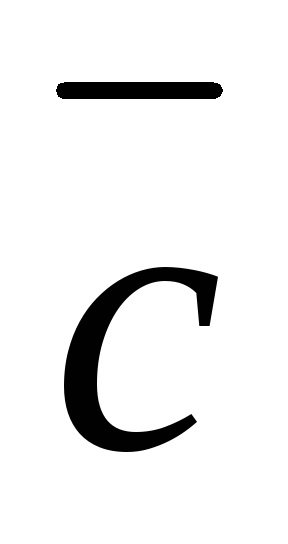
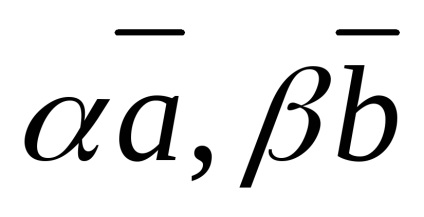
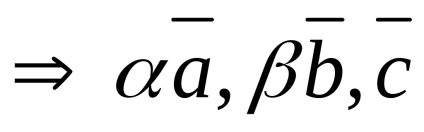
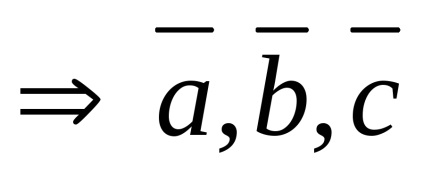
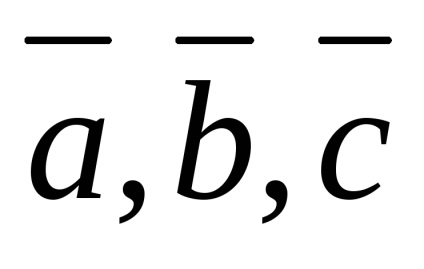
Nulla vektor egy síkban bármely két vektor.
Ahhoz, hogy a vektorok
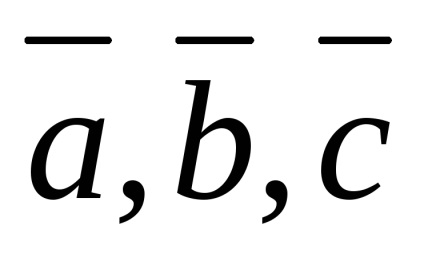
Bármely olyan vektor, sík lehet képviselt lineáris kombinációjával bármely két noncollinear vektorok ugyanabban a síkban.
Bármely négy vektorok tér lineárisan függő.
fontolja 4 esetben:
Ha között vektorok a zéró vektor. Ezután a rendszer lineárisan függ a 2. tétel.
Ha körében vektorok legalább 1 pár kollineáris vektor. Ezután a rendszer lineárisan függ a Tétel 5 és 3.
Ha az egyik vektorok koplanáris hármas vektorok. Ezután a rendszer lineárisan függ a Tétel 6 és 3.
Ha nincsenek nulla vektorok vektorok közül egyenesbe pár és egy síkban háromágyas. Mi kell alkalmazni ezeket a vektorokat 4 tochkeO.
. Rajzolj egy sík vektorok. Ezután a gép a vektorok és a vektorok síkban. Majd felhívjuk áthaladó sík tochkuD párhuzamosan pár vektorok; ; volt. Gyalúkhoz keresztező vonalak kiépítése parallelepipedOB1D1C1ABDC.
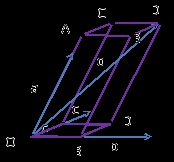
Tekintsük OB1D1C1 - paralelogramma adottak a paralelogramma szabály.
Tekintsük OADD1 - paralelogramma (téglatest tulajdonságait), míg
By 1. tétel
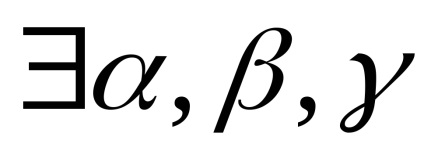
A összege a három nem egy síkba eső vektorok egy olyan vektorban, amely egybeesik egy átlós a paralelepipedon által alkotott Ezt a három vektort alkalmaznak a közös eredetű, az elején a vektor összeg egybeesik a közös eredetét e három vektorok.
Ha a hely, hogy három noncoplanar vektor bármely vektor ezt a helyet bontható lineáris kombinációja a három vektor.