A megoldások példái a Cramer-módszer
1. példa Az egyenletek rendszerének megoldása Cramer módszerrel
Először összeállítjuk és kiszámítjuk a rendszer fő meghatározóját:
Mivel a rendszernek egyedülálló megoldása van, amelyet Cramer szabálya szerint találhat:
ha azokat a meghatározóból szereztük be az 1., 2. vagy 3. oszlop helyett a szabad feltételek oszlopával.
Tehát az egyetlen megoldás.
2. példa Az egyenletek rendszerének megoldása Cramer módszerrel
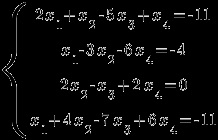
Tegyük fel a rendszer fő meghatározóját:
A determináns tulajdonságainak felhasználásával az első oszlop nulláit hozunk létre. Ehhez,
- A második és a harmadik sor változatlan marad,
- Szorozzuk meg a második sort -2-vel és adjunk hozzá az elsőhöz
- Szorozzuk meg a második sort -1-vel és adjunk hozzá a negyedikhez
Ezen konverziók után a determináns értéke nem változik, de a következő formában írja be
Most, a meghatározó definíciójának felhasználásával és a negyedik oszlop elemeinek kibővítésével kapjuk meg:
Így az egyenletek rendszerének meghatározó tényezője nullától különbözik. Cramer szabálya szerint egy ilyen rendszer egyedülálló megoldást kínál. Találjuk meg. Ehhez négy további tényezőt hozunk létre és számolunk ki:
Kramer szabálya szerint megoldásunk van:
Tehát az egyetlen megoldás.