Mi a geodéziai kupola
Ebben a cikkben megpróbáljuk leírni, mit jelent a geodéziai kupola egyszerű szavakkal. Valójában a geodéziai kupola olyan rács, melyet "gömb alakú" (polyhedra) halmazból állítottak elő, amely a lehető legközelebb áll a gömb alakjához.
Ha alaposan megnézed, a háromszögek a rács alapjává váltak, nem pedig rombusok, négyzetek vagy hexahedronok. A háromszöget a legstabilabb és erőteljesebb geometriai struktúra választotta ki. Tehát a háromszögek (esetünkben a geokupol) szerkezete nagyon erős és önálló képességekkel rendelkezik. Maga "megtartja" magát, mint szerves struktúra. Minél több arcot használunk felépítésre, annál erõsebb a rácsunk és a simább alak.
A geodéziai kupolát alaposan megvizsgálva nyilvánvalóvá válik, hogy a geodéziai hálózat felépítése nem kaotikus, hanem szigorú matematikai modell. Ez a modell a Platonos szilárd anyagok geometriájából származik, a rendszeres poliéderek, melyeket a tudósok fedeztek fel a távoli múltban.
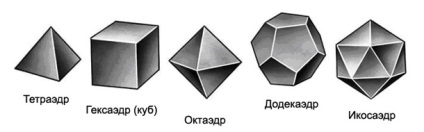
A geodetikus kupola felépítése a Platóni testeken alapul, amelyek közül öt van, de az Icosahedrónak csak a leggyakoribb változatként tekintünk részletesen. Az icosahedron egy rendes poliéder, amely 30 azonos szögből áll, amelyek 20 egyenlő oldalú háromszöget hoznak létre.
Gondoljunk tehát egy geodéziai kupola kialakítására szakaszokban:
1. Először egy adott sugárral rendelkező gömböt készítünk

Ezután építsük az icosaedert "beírva" a gömbbe. Ebben az esetben az icosahedron mind a 12 csúcsa a gömb felületén fekszik. Minden háromszög azonos.

3. Mert az icosahedron minden háromszöge egyenlő, közülük bármelyiket választjuk és kisebb egyenlő oldalú háromszögekre osztjuk. Esetünkben a lebontás az ötödik frekvencián történik (ezt később tárgyaljuk). Az icosahedron kiválasztott kezdeti háromszöge kisebb háromszögek 5 "soraira oszlik. Így kiderül a "lapos" bontás a rács.

4. Ebben a szakaszban a gömb középpontjából érkező szegmenseket építjük. Ezeknek a szegmenseknek át kell haladniuk a kapott rács összekötő pontjain, és a gömb felületén kell végezniük.
5. Ezután összekapcsoljuk a gömb felületén lévő szegmensek csúcsait. Van egy háromszög alakú szerkezete, amelynek csúcsa a gömb felületén fekszik, gyakorlatilag megismétli a formáját. mert az icosaéder összes eredeti háromszöge ugyanaz, akkor biztonságosan másolhatjuk a kapott rácsot, megkapjuk a kívánt geodetikus kupolát vagy gömböt.

A geodézikus dóm háromszögelésének gyakorisága
A "frekvencia" vagy a "háromszögelési gyakoriság" fogalmát gyakran a geokupol számításaiban találjuk meg. Ez azt jelenti, hogy a kupolát háromszögekre törik. Ie Egy és ugyanazon kupola leírható a különböző háromszögek számával. Például egy kevésbé sűrű partíciónál kevesebb háromszög szükséges, de hosszabb élhosszúsággal, és az alak jobban szögletes lesz. A sűrűbb elrendezéshez további háromszögek szükségesek, kisebb élhosszúsággal, de az alak egyenletesebb lesz és közel lesz a gömbölyűhöz.
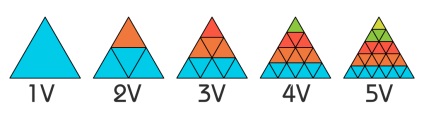
A világ az "V" latin betű szabványos frekvenciakijelölését használja. Az alábbiakban példák a háromszögelésre az ötödik értékre. Amint észre fogod venni, a frekvenciaérték száma megegyezik a "sorok" számával, amelyekbe az icosaéder háromszögek egyikét felosztják.
Milyen gyakorisággal választhatja ki a geodéziai kupoládat az Ön számára. Ez a paraméter számos paramétertől függ: a kupola mérete, a csapágy és az egyéb tulajdonságok, az élek hossza, a gazdaság és az esztétika.
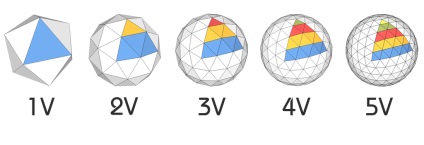
Egy gömb keresztmetszete
A következő paraméter, amelyet mindenkinek tudnia kell a geodéziai kupola kiszámításánál, a gömb keresztmetszetének értéke. Ha figyelembe vesszük a gömb egészét, akkor más részekre oszthatjuk. mert a geodéziai "lebontás" sorokból áll, akkor a legalkalmasabb az ilyen sorok kupéinak megtörése. Különböző "V" frekvenciájú kupolákkal - különböző "sorok" száma, ezért a részük mindig egyedi. Az alábbiakban néhány példa a különböző frekvenciájú kupolákról.
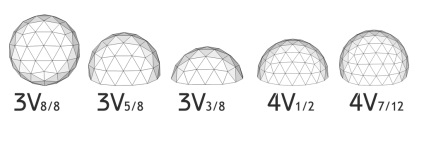
Láthatja és tanulmányozhatja a más platronikus testeken (oktaéder, kocka stb.) Alapuló geodetikus kupolák építési módjait ezen a linken