Descartes fa implicit kulcs segítségével
[szerkesztés] Alapvető ötlet
Vegyünk egy adatstruktúrát dinamikus tömbként. A szabványos végrehajtását, képesek vagyunk hozzá elemeket a végén a vektor, hogy ismerjék el az elem egy bizonyos helyzetben, hogy módosítsa a tárgy által és eltávolítja az utolsó elem. Tegyük fel, hogy szükségünk van egy adatstruktúra a fenti tulajdonságokat, valamint műveleteket: Elem hozzáadása olyan helyen (a megfelelő változást elemek számozás), és eltávolítható bármely elem (szintén számozása pedig megfelelően módosul). Egy ilyen szerkezet lehet megvalósítani alapján a derékszögű fa, az eredmény gyakran nevezik a derékszögű implicit kulcs elemét (Eng. Treap implicit kulcs).
[szerkesztés] X gomb
Mint tudják, egy Descartes-fa olyan adatszerkezet, amely kombinálja a bináris keresési fa és a bináris gyűjteményt. A Descartes fa implicit kulcs segítségével történő végrehajtásakor módosítjuk ezt a struktúrát. Nevezetesen csak a prioritást hagyjuk benne, és a kulcs helyett a következő mennyiséget használjuk fel: az elemünknek az elemünk bal oldalán található elemeinek száma. Más szavakkal kulcsfontosságúként vesszük fel a fa elemének rendszámait, egyenként csökkentve.
Ne feledje, hogy ez megőrzi a bináris keresési fa struktúráját ebben a kulcsban (vagyis a módosított Descartes-fa továbbra is Descartes-fa marad). Ezzel a megközelítéssel azonban probléma merül fel: az elemek hozzáadásának és eltávolításának műveletei megváltoztathatják a számozást, naiv módon pedig minden kulcsváltozás időbe telik, hol van a fa elemeinek száma.
[szerkesztés] A C segédérték
Ez a probléma egyszerűen megoldódott. A fő ötlet az, hogy maga a kulcs nem tárolható sehol. Ehelyett egy kiegészítő értéket tárolunk: a csúcsok száma a csúcsunk szubtrófelében (maga a csúcs szerepel a részfelületben). Figyeljünk rá, hogy a rendes Descartes-fa műveletek felülről készültek. Szintén fontos megjegyezni, hogy ha az út a gyökértől néhány csúcsot összeadják ezeket az értékeket a bal oldali részfa ahol mi nem megy, plusz egy, aztán jött a csúcsra, és hozzátéve, hogy az érték az elemek száma a bal részfa, megkapjuk a ha ez a kulcs.
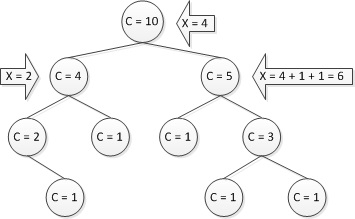
[szerkesztés] A Descartes-fa szerkezetét támogató műveletek
Hagyományos Descartes fa struktúra támogatja révén két művelet: - particionálás egy Treap két olyan, hogy az egyik legfontosabb kevesebb, mint egy előre meghatározott értéket, és a többi - nagyobb és - egyesülő két fa, amelyek közül az egyikben az összes kulcsok kevesebb, mint a másodikban. Mivel a különbség a derékszögű fa implicit kulcsot a normális, a műveleteket a következőképpen írható le: - válaszfal fa két, hogy a bal lesz pontosan a felső, és - az egyesülés bármely két fa, ill.
[szerkesztés] Split
Hagyja, hogy az eljárás a fa gyökerén kezdődjön, és a csúcsfát le kell vágnia. Az is ismert, hogy csúcsok vannak a csúcs bal oldali részfelületében és a jobb oldali részfelületben. Tekintsünk minden lehetséges esetet:
- . Ebben az esetben rekurzív módon kell elindítani az eljárást a bal fiúval azonos paraméterrel. Ugyanakkor a gyökér új bal fia a rekurzív eljárásra adott válasz jobb oldala lesz, és a válasz gyökere lesz a megfelelő.
- Az eset szimmetrikus az előzőhöz képest. Rekurzívan, az eljárást a megfelelő fiúval végezzük egy paraméterrel. A gyökér új jobb fia a rekurzív eljárásra adott válasz bal oldala lesz, és a válasz gyökere balra lesz.
[szerkesztés] Egyesítés
Lássuk az eljárás bármely megvalósítását. Ne feledje, hogy a program soha nem fér hozzá a kulcshoz. Ezért egy Descartes-fa eljárásának végrehajtása implicit kulcs segítségével egyáltalán nem térhet el ugyanarra az eljárásra egy közönséges Descartes-fában.
[hivatkozás szükséges] A C értékek helyességének fenntartása
Az egyetlen olyan intézkedés, amely biztosítja ezeknek az értékeknek a helyességét, hogy a tetején lévő gyermekekkel végzett bármely cselekvés után be kell írnia a területére az értékek összegét új gyermekeiben, egyenként.
[szerkesztés] A leírt fa alkalmazása
Így le van írva egy szerkezet, amelyből egy tetszőleges hosszúság egy részét balra lehet levágni, és két tetszőleges részt egyesíteni a kívánt sorrendben. Most van lehetőségünk:
- helyezze be az elemet bárhová (vágja el a bal oldali elemek megfelelő mennyiségét, illessze be a bal oldalt a faval egy hozzáadott elemből és az eredményt - a megfelelő fa segítségével)
- a tömb bármely részének átrendezésére bárhol (a szükséges sorrendet elvégezzük és a helyes sorrendbe illeszkedünk),
- csoportos műveletek végrehajtása elemekkel. Emlékezzünk ezekre a műveletekre a szegmensek faibe, és megértsük, hogy semmi sem akadályoz meg minket abban, hogy ugyanezt tegyük a leírt fához. A csoportmunka során természetesen a funkció a szegmensből származik,
- ha két fát készít ugyanarra a forrás-tömbre a különböző paritású elemekből, megoldhatja azt a problémát, hogy az egyenletes és páratlan helyek helyét egy szegmensre változtatják,
- a Descartes-fa elképzeléseit implicit kulcson felhasználva, olyan adatszerkezetet valósíthat meg, mint a kötél.