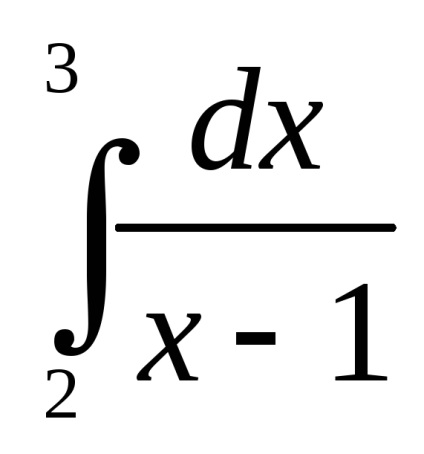Az akkordok módszere

Egy meghatározott integrál kiszámításához

használja a formanyomtatvány kvadratúra formuláit

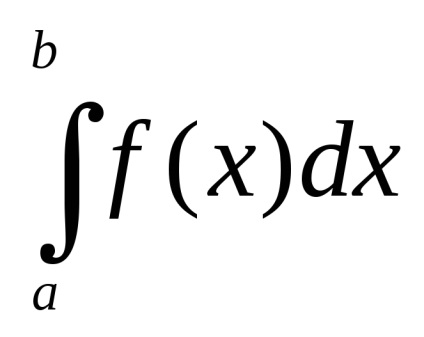
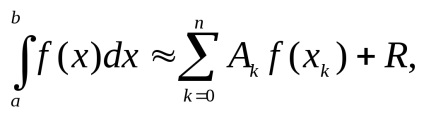
ahol xk és Ak a kvadratúra-képlet alapján határoznak meg, R a maradék kifejezés vagy a kvadratúra-képlet hibája.

Az integráció szegmense [a, b] n egyenlő részekre van osztva egy egyenlő pontok rendszerével xi = x0 + ih. ahol i = 0,1,2. N; x0 = a, xn = b.

A partíció lépése. Ezután kiszámítjuk az integrandot a kapott csomópontokban: yi = f (xi).

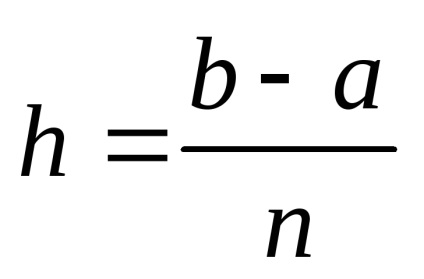
Kvadratúra formulák az egyenlő távolságra lévő csomópontokhoz:

1) a bal oldali téglalapok képletét:

ahol yi = f (xi), xi = a + ih;

2) a jobb oldali téglalapok képletét:

ahol yi = f (xi), xi = a + ih;

3) a központi téglalapok képletét:

ahol yi = f (xi),

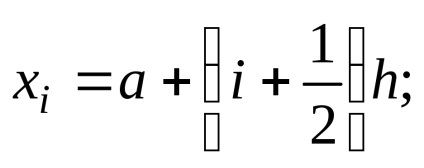
4) a trapéz alak:

ahol yi = f (xi), xi = a + ih;

5) Simpson formula (parabola képlet):

ahol yi = f (xi), xi = a + ih.

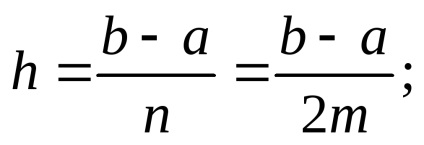
6) Newton-képlet (szabály

):

ahol yi = f (xi), xi = a + ih.

.

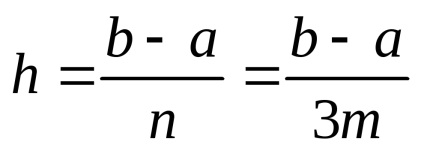
Az integrálokat kvadratúra-képletekkel kell pontossággal használni. A számítás szükséges pontosságának eléréséhez . a kettős számolás módszerét alkalmazzuk. Az integrált értéket a választott kvadratúra-képletből számítjuk kétszer, először egy h lépéssel. majd lépésekben

, azaz duplázza meg az n számot (a partíció pontjai száma [a, b]).

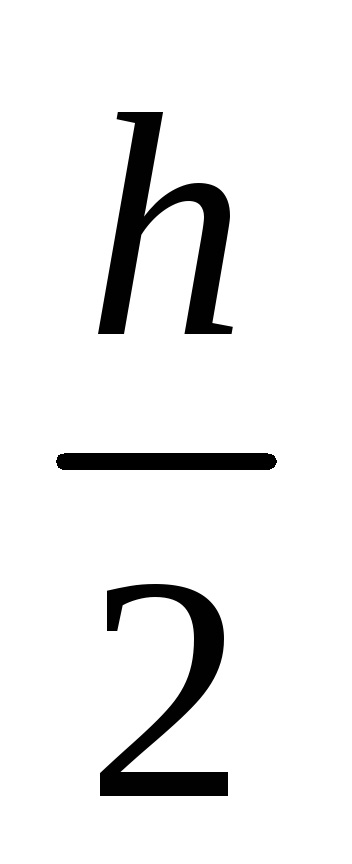
Jn és J2n partíciók eredményeit jelöljük, és hasonlítjuk össze őket. Ha | Jn-J2n |<. где  – погрешность вычислений, то в качестве результата берут J2n . Если |Jn-J2n|. то вычисления повторяют с шагом

és így tovább.

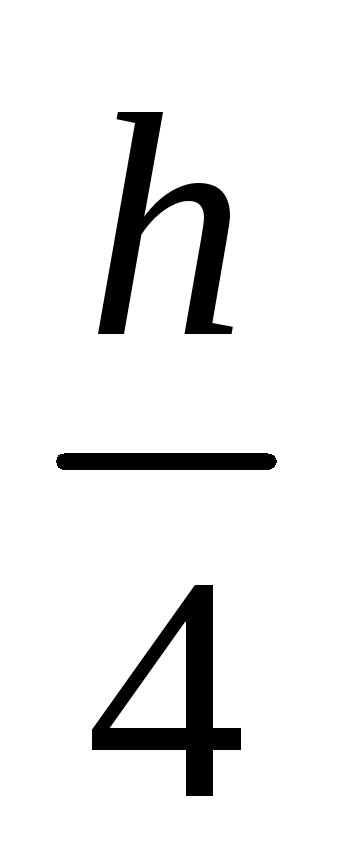
Egy példa. A trapéz alakú képlet segítségével számítsa ki az integrált értéket

pontossággal  = 0,01.

Kapcsolódó cikkek

• 3) R28 - cementaktivitás, standard módszerrel meghatározva (a 4 - 81 állapot szerint), t

• Mts vagy kereskedési módszer

• A skvortsov módszerével megragadtuk a skvortsov módszerét