A konfiguráció
- egy véges sor pontok, vonalak, síkok kölcsönös előfordulása. K lehet sík és térbeli.
A lapos kialakítású, - végső rtochek gpryamyh rendszer és a sík, rendezett, hogy minden ponton a rendszer incidens azonos számú makacs ez a rendszer, miközben bármelyik vonal incidens az azonos számú p pontot a rendszer. Minimális pontrendszer adott K. raj teljes K. úgy állíthatjuk elő, az előfordulási pontpárok egyenes vonalakkal és metszéspontjai párok nevezzük. generáló rendszer a K. A számok p, g, g, o kapcsolódó pg = g p, a K. jelöljük (R g, gp). K, amely azonos számú pontot és vonalat tartalmaz, a szimbólum (p y) jelöli.
Példák a K. síkra. 1) Egy pontot és egy egyenes vonalat alkotnak egymásnak K. (11). 2) Három pont, amely nem fekszik egy sorban, és mindegyik párhoz három vonal keletkezik, K. formából (32),
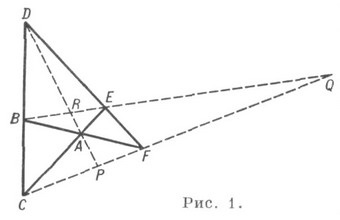
ez a szám három csúcs (vagy háromoldalas) a síkon. 3) A teljes négyszög négy egyenes vonalú és hat puszta keresztmetszetű K alakja (62. 43). Azonban itt nem minden K. vonal összekötő párospontja egyenes egyenes ebből a K-ból; az R, P, Q és az RP, RQ, PQ pontok nem tartoznak hozzá (1. ábra).
Egy automorfizmus a. a K leképezése önmagára, ahol K a pontok felé halad, egyenes vonalakat ugyanannak a K-beli egyeneseknek. Ebben az esetben nincs semmiféle incidencia, és nincsenek újak. K. felhívta. Helyes, ha a K automorfizmus csoportja tranzitív.
Egy adott K. (pg, gp) esetében a kettős K. (gp, pg). K típusú (pg) típusú K, és csak ilyen, a kettő azonos típusú K-nak felel meg, ezeket hívják. kettős invariánsak.
K. felhívta. projektív, ha elemeinek előfordulása a projektív átalakítások alatt megmarad. Például. előfordulási gyakorisága egy bizonyos elemek raj K. található, a projektív sík biztosítja a kapcsolatot annak axióma, ezért az előfordulási pontok és vonalak K. tartósított e sík projektív transzformáció, és projektív K. lesz. A K. sík összes incidensét és elemeit a rajzon csak egy vonalzó segítségével lehet ábrázolni. A lapos K. mindig kettős, a dualitás elve miatt.
K is definiálható véges rész síkként. Egy bizonyos K. létezését a geom határozza meg. valamint a pontok és vonalak száma és a kölcsönös események száma közötti kombinatorikus kapcsolatok. A K-t absztrakt sémákkal is definiáljuk, például négy pont, A i csúcs és négy sík incidensek (négyszög keresztmetszete), a tetraéder Di-arcai a táblázatban jelennek meg. Miután a K. definíciója absztrakt módon megfogalmazódott, felmerül a kérdés, hogy megvalósulnak-e, vagyis az összes incidensnek egy adott generátorrendszerben való felépítésének lehetősége. A felület finom részterülete megvalósíthatósága azt jelenti, hogy egy izomorf térkép egy sík egyes alplánjára lehet.
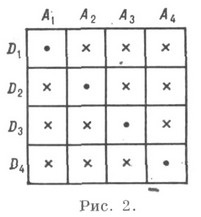
K (p 2), p-adherens formában valósul meg, oly módon, hogy a csúcsai és oldala párosan járulékos. A K. (32) absztrakciót például úgy lehet megépíteni, táblázat, mint a 2. A K (p 3) sík csak akkor lehetséges, ha minden egyes K ponton három egyenes vonalat kell áthaladni, és mindegyikre két további K pont kell feküdnie (a p számnak meg kell felelnie az egyenlőtlenségnek). K típusú (p 3) módosítható, amelynek száma p. K. (73) egy séma (3. ábra),
ahol a számos zárójel azt jelenti, egyenes metszéspontja áthaladó pár pont a baloldalon a konzolok számát függőleges sávok jelölik pontok to- legyen egy egyenesen, ha az összes szóban forgó bal előfordulása. Az igazi projektív síkon az összes incidens teljes négyszeresben valósul meg (4.
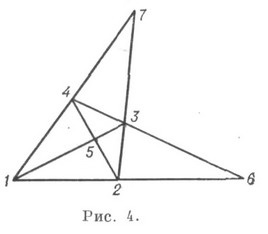
Azonban az utolsó incidencia (a három pont kolinearitása) itt nem történik meg. K. (93) három különböző módosítást ismer fel, amelyek közül az egyik (93) 1. a Brianchon-Pascal konfiguráció (5. ábra): mindegyik egyenes vonal három különböző ponttal, a, - és minden egyes ponttal - három különböző vonalon.
Ez a K megvalósítható a projektív síkon (6. ábra), projektív, szabályos, kettős invariáns (lásd Bryanshon tétele, Pascal tétel).
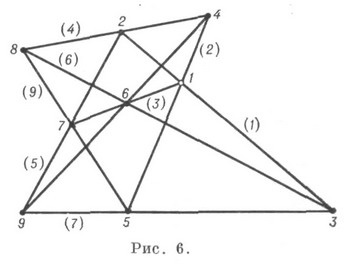
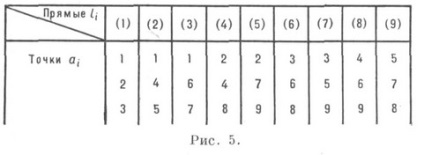
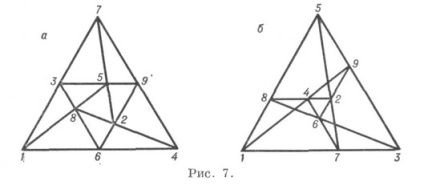
Két másik módosítás a K. (93) 2-ben. (93) 3 (7. ábra) jelentősen különbözik a Brianchon-Pascal konfigurációtól. Például. K (93) 3 nem szabályos, és a K (93) 2 megépítéséhez szükség van egy másodrendű segédgörbére.
K. (103) tíz különböző módosítással rendelkezik, amelyek közül a legfontosabb a Desargues alakja (8. ábra).
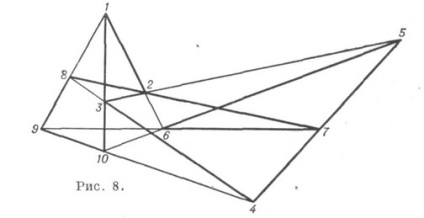
A valós projektív síkon valósul meg, projektív, rendszeres, kettős invariáns. A másik kilenc módosítás. (103) általános geometriát nem mutat. tételeket, és csak nyolcat lehet megvalósítani az igazi projektív síkon, de a létrehozásukhoz szükség van egy generációs pontrendszer speciális elrendezésére (különösen ez a K rendszeres rendszeres szorzók formájában valósul meg (9.
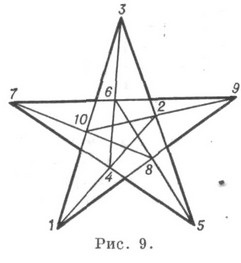
A rajzon feltüntetett csúcsok sorrendjében egy ívelt és egyidejűleg leírt tízoldalas is található. K. (93) és (103) szintén megadják a geometriai értékeket. (93) 1 kilenc oldalú személy (2, 3, 6, 1, 5, 9, 4, 8, 7, 2) (lásd a 6. ábrát) , a Desargues alakja - tíz oldalú (8. ábra) formájában (1, 2,3,4,5,6, 7, 8,9, 10, 1). Ezeknek a K.-nek az ábrázolása egyedülálló az automorfizmusokra. Általában a p-adherensek építése, amelyek egyidejűleg be vannak írva és körülírva magukról, a K. típusú típushoz (p3) vezetnek. A K. típusú (p 3) ábrázolások is több egymás köré írt és leírt többszöröző formájában vannak.
Például. Desargue konfiguráció lehetővé teszi egyetlen módja (akár automorfizmusa) egy pár, egymáshoz beírt és körülírt pyatistoronnikov (1, 9, 7, 5, 3) és a (8, 4, 10, 6, 2) (ábra. 8). A szám növekedésével a K. típusú módosítások száma (p 3). gyorsan növekszik.
Térbeli konfiguráció - véges pontrendszert és különböző síkok, hogy mindegyik pont incidens azonos számú síkok és minden síkon - az azonos pontok számát. A pontokkal és síkkal alkotott K.-vel együtt a tér pontokból és vonalakból áll. Tehát a fent tárgyalt konfigurációs Desargue álló pontokból és vonalakból is prededavlyaet térbeli K. (103) (8. ábra), ha a megfelelő trehstoronniki hazugság különböző síkokban; ugyanabban az időben úgy tekinthető, mint K. (103. 56), amely a pontok és síkok, hat megfelelő csúcsokat trehstoronnikov, perspektivikus központ és három pontot a kilátásai egy tengely a k-ryh konvergálnak trehstoronnikov érintett felet, hogy összesen tíz pontot és három síkban kialakítva a felek által trehstoronnikov, és két sík trehstoronnikov magukat adni az öt sík. Minden síkban hat pont található, és minden pont három különböző síkra esik.
A triviális űrhajó a típus (p g). K. (43), a sémája a 3. ábrán látható. 2; ezt egy tetraéder képviseli. K típusú (p 4) nem lehetséges, p = 8 esetén öt különböző séma van, az egyik a k-es, az ún. A Mobius-konfiguráció két tetraéderből áll, amelyeket egymás mellé írt és leírtak. Mind a nyolc pont - a tetraéderek csúcsai - a négy tetraéder arcának négy síkjával jár, és mind a nyolc sík négy ponttal - a csúcspontokkal. Ha egy magasabb rendű K-hoz fordul, a lehetséges módosítások száma gyorsan növekszik, például, K. (94) már 26 geometriai alakot tartalmaz. megvalósítható módosítások.
A K. térbeli magasabb rendű méltó konfiguráció és Reye Schläfli konfiguráció. A Reye konfiguráció neve. amely K. pontból és síkból áll (126). Egy valódi projektív térben meg lehet építeni, például, egy bizonyos csúcsa egy kocka-ságot a közepén, a három (végtelen) pont k-ryh konvergálnak párhuzamos élei a kocka, és a repülőgépek, amelyek K. hat kocka arcokat és hat annak átlós síkok áthaladó egy pár átellenes szélei (ábra. 10 ).
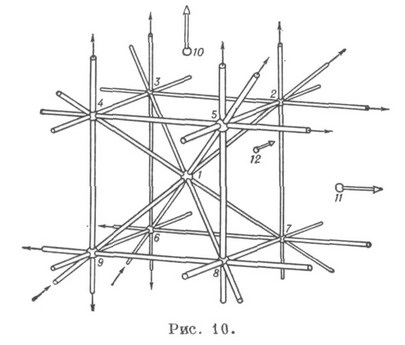
A Reye-konfiguráció projektív, szabályos és kettős invariáns, és ennek a K.-nek a képét (a nagy kettősség elvének megfelelően) lehet egy oktaéder helyett egy kocka helyett (11. ábra).
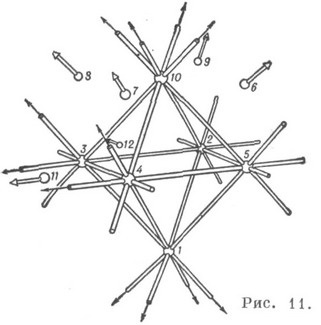
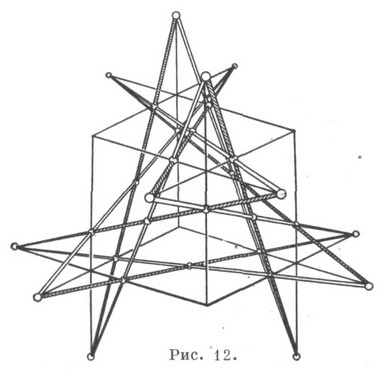
A Reye-konfiguráció térbeli K pontnak és egyenes vonalnak (124.163) is tekinthető. K. (302. 125), amely pontokat és egyenes vonalakat tartalmaz. egy dupla, hatoldalú Schlafli. Ez például a térben van ábrázolva. szimmetrikusan elrendezett egyenes vonalak és pontok formájában a kocka mindegyik oldalán (a kettő közül az egyik) (12. ábra).
Nem minden lapos K. megvalósítható az igazi projektív síkon. Például. (73) és (83) nem valósul meg rajta, és ezzel összefüggésben a probléma merül fel a K bármely más projektív síkon való megvalósításában. Minden mondat. kijelentve, hogy egy bizonyos K. adott síkban való megvalósíthatósága minden esetben, kivéve talán talán egy esetet, az R összes valószínűtlenségét jelenti, az adott sík konfigurációs javaslata. Így ha egy bizonyos K eseményei egy adott síkban realizálódnak a sík geometriai tulajdonságai miatt, akkor K ezen a síkon valósul meg. Például K. (93) 1. mindig az igazi projektív síkon valósul meg, hiszen az összes kivételtől eltekintve, kivéve az egyiket, az utolsó előfordulás mindig elégedett Brianchon és Pascal tételei miatt, vagyis ezek a tételek konfigurációs javaslatok. A K. (73) (4. ábra) utolsó eseményének teljesítése nem történik ilyen síkon (mivel a teljes négy csúcs átlós pontja nem ugyanarra az egyenesre tartozik), ezért ez a kijelentés nem konfigurációs javaslat. Azonban ez lesz a komplex projektív síkon. Hasonlóképpen, más C; különösen K. (83) véges pápai síkokban valósulhat meg, amelyek három és négy elemet tartalmazó Galois mezőkön épülnek fel.
Az adott síkon érvényes konfigurációs javaslatok bizonyos értelemben szervezik ennek a síknak az elemeit, és ezért szerepet játszanak a sík geometriájának axiomatikus felépítésében. Például. ha az adott síkban teljesülnek a projektív sík összekapcsolásának összes axiómái, de a Desargues konfiguráció megvalósul, akkor ez a sík viseli az úgynevezett " nem megkülönböztető geometria. A konfigurációs mondat is algebrai formában írható. formája bizonyos algebrai formában. identitás. Egy tetszőleges projektív síkon a konfigurációs javaslatokat csak új axiómákként lehet bevezetni, és egy vagy másik konfigurációs javaslat megfogalmazása más konfigurációs javaslatok érvényességét vonhatja maga után. Általánosságban elmondható, hogy minden algebrai. A konfigurációs javaslat megfelel az azonosítónak. geometrikus. e identitás ábrázolása egy bizonyos síkon, ahol K valósul meg (azonban nem derül ki, hogy bármilyen konfigurációs javaslat egy bizonyos fajta identitás geometriai reprezentációja a projektív sík ternerének és természetes testének algebrájában). Az ilyen algebrai kutatás. ekvivalensek lehetővé teszik mind a kvantummechanika tulajdonságainak vizsgálatát, mind a véges részleges sík megvalósíthatóságának lehetőségét egy meghatározott projektív síkon, valamint a különböző konfigurációs javaslatok közötti logikai kapcsolatot.
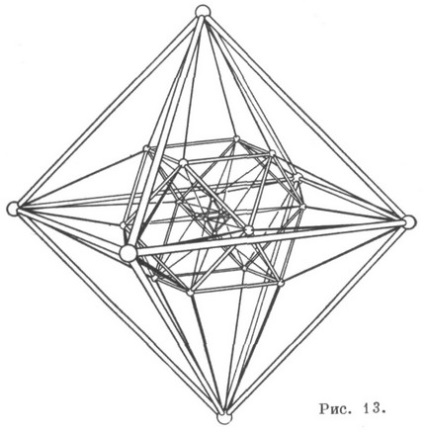
A kvantummechanika elmélete számos geometriai problémát megold. kérdések. Így egy K. (83) sík fontos szerepet játszik a harmadik sorbeli síkgörbék elméletében, amelyek nem rendelkeznek dupla ponttal, különösen az inflexiós pontjaik tanulmányozása során. A Reye-konfigurációt a rendszeres polyhedrák tanulmányozására használják a négydimenziós euklideszi E 4 térben. Az E 4 rendszeres polyhedronját olyan tartományok határolják, amelyek rendszeres háromdimenziós poliéderek. Rendszeres polytopont hívunk az E 4-ben. n-sejtet, ha korrekt polyhedrával van határolva. Például. 5 háromdimenziós sejt korlátozódik öt tetraédert, 8-cellás - .. nyolc kocka, stb, ahol az 5-sejt és 24-sejt kettős maguk (a pontok megfelelnek a terek, és a vonalak - síkok). A helyes sejtek tanulmányozását az E 3-as vetületek tanulmányozásával végezzük. Ha a vetülete a tér kiválasztott 24 cella nek-paradicsom trehmernayagran kiderül, a szétválás a helyet a 12-octahedra, amelyek közül az egyik az összes, kivéve a középső szakaszon a végtelenbe. ami a Reye-konfigurációt képező kivetítés egyik formájához vezet (10. Ha a háromdimenziós tér a vetítési tér. a 24 cellának csúcsán áthaladva, akkor a Peee-konfiguráció is létrejön (11. ábra). (A 24 cellának háromdimenziós térre való kivetítése a 13. ábrán látható)
A Reye-konfiguráció szintén megjelenik a négy golyó hasonlóságú pontjaiban és tengelyeiben, amelyek középpontjai nem egy síkban fekszenek. Ebben a rendszerben minden tengely három ponttal jár, és minden pont négy tengellyel, térbeli (124.143) ponttal és egyenes vonalat kap. Minden három pont - a hasonlóság központok - meghatároz egy síkot, minden két tengely incidens hasonlóságokat pont alkotnak nyolc különböző síkok, 12, melyek mindegyike az incidens hat pont a hasonlóságot, mivel mind a tizenkét hasonlóság pont - hat azaz a K.-t kapjuk (126). K, amelyet a kettős Schlafli hexagram képvisel, az algebrai polinomok tulajdonságainak tanulmányozására szolgál. a harmadik sor felszínét, amelyet 19 pont határoz meg és mindig egy bizonyos kétoldalas hatoldalú Shlefli-on halad át. Lényeges, hogy a négy egyenes vonal hiperboloidális elrendezéssel rendelkezzen.
A konfiguráció javaslat végrehajtásában az előfordulási a gépen használt a tanulmány a tulajdonságait mnogostoroynikov (mnogovershinnikov) és oldatokat építési problémák alapján különböző megszorítások (megközelíthetetlen épület elemeinek egy sorban, és így tovább. D.). K. polyhedra elmélete gyakorlati alkalmazást talál a kinematikában és a grafikus statikában.
Lehetséges K. más geometrikus elemekből áll. elemek, például a tetszőleges dimenzióból és az egység sugarától E n-ben.
Irod : [1] Gilbert D. Koi-Vossen S, Vizuális geometria. per. vele. 2 ed. M.-L. 1951; [2] L. Skornyakov, "Uspekhi Matematicheskikh Nauk", 1951, 6. kötet, 6. o. 6, p. 112 154; [3] BI Argunov, "Matematical Collected Materials", 1950, 26. old., 3. szám, p. 425-56; [4] Levi F. Geometrische Configurationenen, Lpz. 1929.
Matematikai Encyclopedia. - M. Soviet Encyclopedia. I. M. Vinogradov. 1977-1985.