Transformers - stadopedia
4.1 A transzformátor elrendezése és működési elve
A transzformátorok olyan készülékek, amelyek feszültséget vagy áramot alakítanak ki (28. Az ilyen eszköz értékét a rendkívül széles körű helyzetek határozzák meg, ahol használják. A transzformátoroknak köszönhetően az elektromos energia megszerzi azokat a formákat, paramétereket és tulajdonságokat, amelyek a leginkább keresettek és kényelmesek az egyedi alkalmazásokhoz. Ugyanakkor emlékeztetni kell arra, hogy a transzformátorok csak AC áramkörökben működhetnek, és egy kis feszültségű egyenáramú áramkörbe való beépítésük is letilthatja őket.
A legegyszerűbb (az intézkedés elvének bemutatásával, de nem építés alatt) a transzformátor három elemből vagy összeállításból áll: 1) az elsődleges tekercs; 2) mágneses áramkör; 3) szekunder tekercselés (29.
Elektromosan a transzformátor mindkét tekercsét egymástól és a mágneskörből elkülönítik. Ez utóbbi masszív ferromágneses magot jelent, amely összeköti a tekercseket és a mágneses csatlakozást. Az elsődleges tekercsbe belépő villamos energiát egy mágneses tekercseléssel alakítják át, amelyet a mágneses áramkörön át a szekunder tekercsre továbbítanak, majd újra elektromos energiává alakulnak, de már a szekunder tekercselésből. A transzformátorban az átalakítás során keletkező energiának egy része elveszik, ami felmelegszik. Az átvitt energia és az elsődleges forrásból vett arány aránya határozza meg a transzformátor hatékonyságát, és a képlet szerint számolják ki. ahol W1 az energia bemenet az elsődleges tekercshez; W2 - a fogyasztó által a szekunder tekercseléstől kapott energia.
A modern transzformátorok hatékonysága eléri a 99% -ot, ami azt mutatja, hogy ezek az eszközök rendkívül hatékonyak, mint a villamos energiaadók.
A transzformátor elve az elektromágneses indukció (EMR) törvényén alapul. Emlékezzünk vissza, hogy a fizikai értelemben egy vortex elektromos mező generálása egy váltakozó mágneses mező által. Matematikailag ezt a törvényt a vortex elektromos mező emf-jének jól ismert formája adja:
ahol # 916; Ф - a mágneses fluxus időbeli változása # 916; t. Ennek következtében a modulo, az EMF megegyezik a mágneses fluxus változási sebességével. Ez viszont azt jelenti, hogy az F és e közötti fáziseltolás 90 0-nál van (ez a tény minden nagyságra és sebességre érvényes). A mínusz jel azt jelenti, hogy az EMF a mágneses fluxussal megegyezik. Maga az EMF fizikailag bármely változatban, amely változó mágneses mezőt burkol (a 30. ábrán - 3 fordulattal), és iránya a mágneses mező növekedésétől vagy csökkenésétől függ.
Tekintsük át a transzformátor működését.
Ha az elsődleges tekercsre váltakozó feszültséget alkalmaznak, egy váltakozó áram jelenik meg benne. A váltóáram pedig váltakozó mágneses mezőt hoz magával. Mivel technikailag az elsődleges tekercs tekercs, annak mágneses mezője koncentrálódik benne (a határain túlmenően a különböző szakaszok mágneses mezői kivonásra kerülnek). gyenge
az elsődleges tekercs mágneses mezője, amely átmegy a mágneses körben, többször is (több száz és ezer alkalommal) saját mágneses mezője erősíti, és az áramkörén keresztül lezárja. Ennek következtében a mágneses áramkör mentén egy jelentős változó mágneses fluxus F. Az EMR-törvény szerint az örvénylő EMF a mágneses áramkör bármely szakaszában keletkezik. Ez az EMF mindenütt a környező térben keletkezik, és mind az elsődleges tekercselésre, a szekunder tekercsre, mind a mágneses áramkörre esik.
A primer tekercs teljesen ellentétes fázisú hálózati feszültség, mivel a már említett előző részekben, a tekercs áram elmarad a feszültséget 90 0. egy örvény területen EMF, viszont lemaradt az aktuális (vagy ami ugyanaz - a mágneses fluxus ) egy másik 90 0-mal. Ennek következtében az elsődleges tekercsben az elektromos mezők ellentétes irányban vannak irányítva. Ennek a konfrontációnak az eredménye kis mennyiségű bemeneti áram (üresjáratban) és a tekercs nagy induktív ellenállása. Ezenkívül minden tekercset és tekercset általában rézből készítenek, amely nagyon alacsony ohmos ellenállással rendelkezik. Ebből következik egy fontos mennyiségi tény - a feszültségcsökkenés (u) minden fordulaton csak az örvényes EMF miatt következik be, következésképpen numerikusan egyenlő ezzel az EMF-rel:
Itt figyelembe vesszük, hogy az elsődleges tekercselés feszültsége egyenletesen eloszlik a kanyarokban, mivel a mágneses fluxus egyenletessége a mágneses áramkör mentén történik.
A mágneses kör EMF indukált elektromos mező generál a keresztmetszeten, örvényáramok (Foucault áramok), amely, ha nem kerül sor intézkedésekre, sokkal alacsonyabb transzformátor hatékonyság és okoz jelentős fűtési a mágneses kör, és még túlmelegedés. Az ilyen áramokkal szembeni ellenállóképességet a szigetelő lakkal bevont vékony lemezekből gyűjtik össze. Ez lehetővé teszi az elektromágneses energia termikus szórásának erőteljes csökkentését és a hatékonyság növelését. Végül, a szekunder tekercselésnél egy örvénylő elektromos mező minden egyes tekercsben indukálja az EMF-et. amely az összes fordulattal összecsavarozva a terminálokhoz feszültség formájában áramlik. ahol N2 a fordulatszám.
Mivel az EMF maga az örvénymezőben kifejezte az elsődleges tekercs feszültségének csökkenését. majd a megfelelő helyettesítést az utolsó képletben a transzformátor kezdeti alakjához érjük el:
Ebből következik, hogy amikor a másodlagos és primer tekercsek fordulatszámának aránya megváltozik, megváltoztathatjuk a feszültségük közötti arányt. Nevezetesen: ha N2
A feszültség transzformációjának meghatározásához egy egyenletrendszert vezetünk be a k:
Az átalakulás együtthatója, valamint a tekercsfeszültség értékei, névleges teljesítménye és hatékonysága a transzformátor egyik fontos technológiai paramétere.
4.2 Transzformátor üzemmódok
Mivel a transzformátor klasszikus kialakításában két tekercs van, amelyek közül az egyik az elsődleges forráshoz van zárva, a második pedig szabad, akkor a működésének két módja lehetséges: a) a szekunder tekercs nyitva van - az üresjárat; b) a szekunder tekercs zárva van a fogyasztóhoz - a működési mód. Ezek a rendszerek jelentős különbséggel bírnak, mivel a második esetben a mágneses áramkör másodlagos tekercseléséből további mágneses tér keletkezik, amely a transzformátor összes elektromos paraméterét érinti. Ezért ezeket a működési módokat külön kell figyelembe venni.
Szükséges megjegyezni a következőket: mivel az elektromos folyamatok a transzformátor számos tényező befolyásolja, és ezek pontos nyilvántartást az ok-okozati szinten a minőségi leírást nehézzé válik. Ezért könnyebb megérteni a transzformátorban zajló folyamatokat absztrakt fogalmak segítségével. Különösen - vektordiagramokon keresztül.
2) a szekunder tekercseléshez
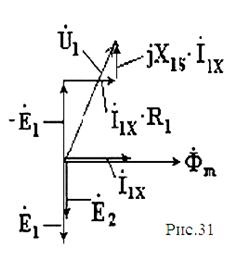
Tekintsünk egy ilyen diagramot készenléti állapotra - az összes tükrözött paraméter fizikai jelentéseinek egyszeri tisztázásával.
Az épület sorrendje a következő:
1) horizontálisan ábrázolja az I1X nem terhelő áram vektorát és a mágneses fluxus Фm mágneses áramkört egymással párhuzamosan. Vákuumban egyetlen fázisban oszcillálnak; a mágneses áramkörben a hiszterézis (a folyadék és a vas mágneses mezejének eltérése miatt) kis mértékű eltérés lehetséges, ami ebben az esetben elhanyagolható lesz)
2) elhalasztjuk az EMR-E1 és E2 örvényáram elektromos mezőinek két EMF-vektorát 90 fokos lefelé (lefelé). Az E1 az EMF-et mutatja az elsődleges tekercsben, E2 - a szekunder tekercsben. Nyilvánvaló, hogy a tekercsek fordulatszámának különbsége miatt ezek az EMF-ek nem egyforma méretűek, és eltérő hosszúságúak.
3) az E1-es vektort az E1-gyel ellentétes irányban ábrázoljuk. Ennek szükségessége az elsődleges tekercs feszültségének egyenletéből következik. Valóban, az Ohm-törvény, amely feszültséget ellenzi EMF EMR E1 (innen a „mínusz” jel), az ohmos ellenállása a primer tekercs R1 (létrehoz egy feszültségesés I1X R1) és az induktív reaktancia, X1. a mágneses mező azon része, amely magába zárja a mágneses áramkör áthidalását (a levegőn keresztül).
4) Az I1X R1 vektort a vektor (-E1) vége felől rajzoljuk - párhuzamosnak kell lennie az árammal, mivel az ellenálláson átesett feszültség mindig egyezik az árammal.
5) az I1X x1 vektort az I1X r1 vektor végéről ábrázoljuk - az áramra merőlegesnek kell lennie, mivel az induktív ellenállás feszültsége mindig 90 0
6) összekapcsolja az E1 vektor elejét az I1X X1 vektor vége felé - az eredményül kapott vektor a vektorok összegét jelenti. azaz U1 vektor.
Az ábrán látható, hogy a pontos ábrázolásnál a vonali feszültség meghaladja az EMP ellenfeszültséget. Azonban a valós transzformátorokban ez a különbség legfeljebb 2-5% az elsődleges tekercs ohmos és induktív ellenállása miatt. A nyitott szekunder tekercselés feszültsége pontosan megegyezik az E2 értékkel. Ezért elégséges pontossággal írhat:
Ahhoz, hogy egy vektort ábrázoljon az üzemmódban, a megfelelő egyenleteket is össze kell állítani. A készenléti üzemmódban levő egyenletektől a szekunder tekercs egyenletének formája alapján különböznek. Ez utóbbit a második Kirchhoff-törvényből is megkapják, és az a forma. Látható, hogy a szekunder tekercselés (U2) feszültsége az üresjárati U2 feszültséghez képest csökkenti az aktív és induktív ellenállások feszültségcsökkenését.
Így a diagram összeállításához a következő egyenleteket alkalmazzuk:
Ezek az egyenletek bonyolítják a diagramok ábrázolásának folyamatát, és annak egyszerűsítése érdekében elhanyagoljuk a tekercsek belső ellenállását. Ekkor az egyenletek nagyon egyszerű formát öltenek:
Az ilyen típusú egyenletektől azonnal következik, hogy az elsődleges és a szekunder tekercsekben fellépő áramok viselkedését illetően nem lehet következtetéseket levonni.
Valójában ezek az áramok szorosan kapcsolódnak a következő okok miatt. Először is, az első egyenletből következik, hogy az üresjárat esetében az örvény mező EMF-nek egyenlőnek és feszültséggel kell szembenéznie a hálózati feszültséggel. Mivel a hálózati feszültség (primer forrás) meg van adva, és nem függ a transzformátor működési módjától, a transzformátor mágneses áramkörében mágneses fluxus működési üzemmódban meg kell egyeznie a mágneses fluxusnak készenléti üzemmódban. Eközben az üzemmódban egyetlen mágneses mező sem mozog a mágneses körben: a szekunder tekercs működési áramlása saját mágneses mezőt hoz létre.
Másodszor, a Lenz-szabály szerint a szekunder tekercs áramának "... olyan iránya van, hogy az általa létrehozott mágneses mező kompenzálja a külső mágneses mező megváltozását". Más szavakkal, a szekunder tekercs mágneses mezőjét az elsődleges tekercs mágneses mezőjével szemben kell irányítani. Ez lehetővé teszi számunkra, hogy a mágneses fluxusok általános egyenletét írjuk le mágneses áramkörökben - vektorokként (!) - formájában:
és figyelembe véve az antiphase karaktert (moduláris formában), mint:
Itt φ0 a primer tekercselés által generált transzformátor mágneses fluxusa üresjáratban; Ф1 - az elsődleges tekercs mágneses fluxusa az üzemmódban; F2 a szekunder tekercs mágneses fluxusa.
Az utolsó egyenlet jelentése az alábbi példával magyarázható. Tegyük fel, hogy készenléti üzemmódban a mágneses áramkör mágneses fluxusa 20 hagyományos egység volt (Ф0 = 20). Ezután, ha a szekunder tekercs működési áramlása mágneses fluxust hoz létre 40 cu (F2 = 40), a primer tekercs a mágneses fluxus, hogy növelni kell a $ 0 = F1 + F2 = 40 + 20 = 60, és csökkenti a teljes mágneses fluxus ismét 20. Ez azt jelenti, hogy van közötti mágneses csatolást áramok a primer és szekunder tekercsek, és az ilyen . hogy a szekunder tekercs jelenlegi növekedése a primer tekercsben lévõ áram növekedéséhez vezet.
Az áramok közötti matematikai kapcsolatot a mágnesesség elméletének alaptörvénye - a teljes áram törvénye alapján - lehet megállapítani. E törvény szerint ". a mágneses tér körforgása zárt kontúr mentén megegyezik az adott kontúron áthaladó áramok algebrai összegével. Mágneses áramkörökkel rendelkező mágneses áramkörök adaptált változatában. a mágneses rugó monogéneként van kialakítva:
Itt az RM a transzformátor mágneses áramkörének mágneses ellenállása; N - a fordulatszám az áramerősséggel, a mágneses áramkör becsomagolása; Én vagyok az áram minden egyes forradalomban; Ф a mágneses áramkör mágneses fluxusa. A képletből következik, hogy:
vagy helyettesítve a mágneses fluxus egyenletébe. kapunk:
vagy RM-re vágva és mindent N1-re osztva:
Az utolsó egyenlet létrehozza az elsődleges és szekunder tekercsekben lévő munkaáramok közötti kívánt kapcsolatot, és egyszerűsített formában lehetővé teszi az üzemmód működési vektor diagramjának megalkotását. Először a következő formában írjuk át:
és tudomásul veszi, hogy az üresjárat kicsi volta miatt az egyenlet jobb oldalán lévő második kifejezés elhanyagolható; akkor az elsődleges és a szekunder tekercsben lévő áramok közötti kapcsolat különösen elkülönül. mert a modulok esetében az egyenlőség tartja. azaz Minél nagyobb a szekunder tekercsben áram, annál nagyobb az áram az elsődlegesben.
A diagram a következő sorrendben készült:
1)
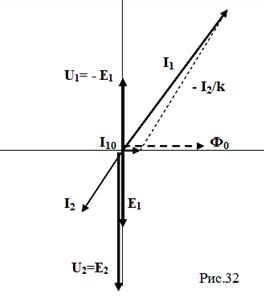
2) rögzítse az elsődleges (E1) és szekunder tekercselés (E2) EMF-jét; azok nagysága a $ 0 értéktől függ. N1. N2; mert Az elsődleges tekercs EMF kisebb, mint a másodlagos, akkor k <1 и трансформатор повышаю-щий;
3) elhalasztja a szekunder tekercselési áramot (I2) - tetszőleges irányban (iránya a terhelés jellegétől függ);
4) a nem-load áramvektor (I10) végén levő jelenlegi egyenletnek megfelelően az (-I2 / k) vektorot ábrázoljuk, és létrehozzuk az I1 összegzett vektort; a vektor (-I2 / k) nagyobb lesz, mint az aktuális I2 vektor;