Térbeli koordináták
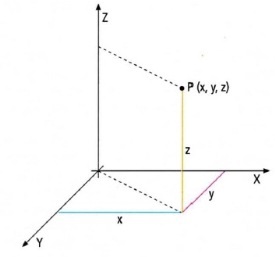
Ugyanígy, ahogy a síkban lévő koordináta-rendszert definiálta, lehetséges egy koordinátarendszert definiálni a térben. Az egyetlen dolog, amit meg kell tennünk, hogy a harmadik tengelyt futtatjuk. amelyet Z tengelynek (z tengely) neveznek. Ez merőleges a másik két tengely által létrehozott síkra. A pontunk harmadik koordinátája az adott tengely mentén a megfelelő magasság lesz.
Azok a problémák, amelyekben a síkok és vonalak érintettek, algebrai módszerekkel megoldhatók.
A tér mérete. Most mutattuk be, hogy az egydimenziós tér egy pontja egy koordinátával rendelkezik: P (x); kétdimenziós térben két koordinátát: P (x, y); és egy pont a háromdimenziós tér által kijelölt három koordináta: P (x, y, z). Ezenkívül egy alsó indexű levél használható a koordináta jelzésére. Tehát a lényeg az egyenes vonal lehet meghatározni, mint $ P (x_1) $, a lényeg a gépen - mint például a $ P (x_1, x_2) $, egy pont a térben - mint például a $ P (x_1, x_2, x_3) $. De semmi sem akadályozza meg, hogy beszéljünk a egy pont koordinátáit a négydimenziós tér - $ P (x_1, x_2, x_3, x_4) $ - és általában egy n-dimenziós térben a pontok formájában $ P (x_1, x_2, ..., x_n) $.
Jelenlétében megfelelő definíciók lehet olyan könnyen egyaránt működnek háromdimenziós 25-dimenziós térben, és még a végtelen - a hiányában matematikai ellentmondás. Már a háromdimenziós térből kiindulva a geometriai intuíció nagyrészt elveszett. ez természetes. Ennek, a többdimenziós terekben is használható algebrai módszerekkel megoldani a problémákat. Persze, nehéz bevezetni, és elismerik a létezését terek, több mint három dimenzióban, de ez nem zavarja a munkát velük matematikai módszerekkel.
Anyagok a témában:
Ossza meg barátaival: