Koordináta rendszer - stadopedia
Amikor dolgozik a háromdimenziós grafika alkalmazott többféle koordináta rendszer. A 2D objektumok megjelenítéséhez egy megfelelő koordináta-rendszerre volt szükségünk, két tengellyel - az X vízszintes tengellyel és a függőleges Y tengellyel. Emlékezzünk arra, hogy a 2D grafika képernyő-koordinátarendszerének kezdete (0,0 pont) van a monitor bal felső sarkában, az X tengely pozitív része az eredet jobb oldalán található, az Y tengely pozitív része alulról.
Együttműködik háromdimenziós tárgyak, szükségünk van egy másik tengely - ez az úgynevezett Z tengely Számos változata a háromdimenziós koordináta-rendszer, különösen a közös úgynevezett jobbkezes és balkezes rendszer. A jobbkezes rendszert használjuk - az XNA keretrendszerben használják. A vázlatos képet az 1. ábrán mutatjuk be. 1.
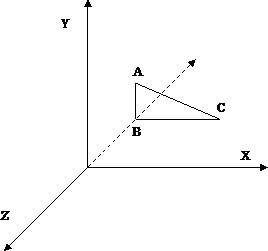
Ábra. 1. Jobboldali koordináta-rendszer
A különlegessége ennek a koordináta-rendszer abban a tényben rejlik, hogy az eredete lehet társítva a bal alsó sarokban a monitor, a pozitív rész az X-tengely, hogy a közvetlenül a származási, a pozitív rész az Y tengely - a felső rész és a pozitív Z-tengely - az elülső. Ez azt jelenti, hogy a látható része a Z tengely - az a negatív része. Ez a része a tengely, mint a „figyelemmel kíséri a mélység”, míg a pozitív része „a monitor előtt.” Az 1. ábrán. 1. a pontozott vonal a Z tengely negatív részét mutatja.
A kétdimenziós koordináta-rendszer, van egy koncepció pont - a koordináták által meghatározott két érték - X és Y pontok léteznek háromdimenziós koordinátarendszerben - ők már meghatározott három érték - X, Y, Z.
A pontok meghatározzák a sokszögek (poligonok) csúcsai, különösen a háromszögek koordinátáit. Így a 3. ábrán látható háromszög. 1. Három pontból - A, B, C
A háromszögek általában bonyolultabb háromdimenziós objektumokat alkotnak.
A háromdimenziós grafikákban van olyan, mint egy arc. Ez egy sík tárgy, amely több csúcsot definiál. A mi esetünkben a szokásos háromszög csak egy arc. Számos sík felületről gyűjthet egy háromdimenziós tárgyat.
Minél több háromszög van a modell megépítésében - annál részletesebben kiderül. A háromszög csúcspontjainak megfelelő, háromdimenziós térben ábrázolható pontokat csúcspontnak nevezik. Talán találkozik a vertex szó többesével: a "csúcs" úgy néz ki, mint a "vertices" angolul. Néha a felsők megjelölésére angol-csúcsú nyomkövetési papírt használnak.
A háromszög nem véletlenül választották az alapvető geometriai formák - első - ez mindig egy sokszög konvex, másrészt - lehetetlen, hogy gondoskodjon a három pontot, így azok nem tartoznak azonos síkban. Azaz, a háromszög - ez a szám, ami mindig domború és sima, amely lehetővé teszi, hogy sikeresen használja céljára háromdimenziós grafika.
Számos arcot, amelyből egy háromdimenziós objektum áll, hálónak nevezik. A "rács" háromszögek készlete.
Egy másik koncepció, amely akkor hasznos, ha a 3D grafikával dolgozik, egy vektor fogalma. Egy vektor, mint egy pont, három paraméterrel definiálható, de nem írja le a helyzetet a térben, hanem a mozgás irányát és sebességét.
A vektor kezdete és vége van, teljes definíciójának ismeretében ismerni kell a vektor kezdetének és végeinek koordinátáit, azaz a három koordinátaérték helyett már hat értékre van szükségünk. Ha azonban eredetileg a származás eredete származik (0,0,0 pont), akkor a meghatározásnak három pontja van.
Például egy vektor, amelynek koordinátái (1,0,0) jelentése: "irány - jobbra, sebesség - 1". Ha elhalasztjuk ezt a vektort a származásról, egyértelműen látható, hogy jobbra irányul (2. ábra).
vektor által meghatározott irányban a helyzetét a második pont képest az első (a mi esetünkben - a helyzet a végpont vektor, ahol a vektor viszonyítva meghatározott eredetű), és a sebessége - a hossza a vektor - amely - a különbség a kezdeti és a végső pont. Esetünkben a vektor hossza egybeesik a végének koordinátáival.
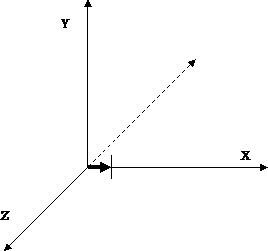
Ábra. 2. A vektor (1,0,0)
Van egy speciális vektor - normál. Normálok építhetők az arcok és a csúcsok egy objektum. Az arcok normáljai merőlegesek ezekre az arcokra. Ezeket egy objektum színének kiszámításakor használják.