Openmp könyvtár
Az OpenMP nem csak egy párhuzamos programozási könyvtár, hanem egy szabvány, amely hivatalosan támogatja a C, C ++ és Fortran nyelveket (és hivatalosan más nyelvekhez, a Free Pascalhoz, például [1]). Az OpenMP csak a megosztott memória architektúrán működik.
Az OpenMP könyvtár úgy van megtervezve, hogy a programozó először írjon egy sorozatot. hibakeresés (elvégre egy párhuzamos program hibakeresése nagyon nehéz), majd fokozatosan párhuzamosan. kiegészítve az OpenMP irányelveket.
Nem titok, hogy a végrehajtási idő nagy része, a programok a ciklusokon belül futnak. Talán ezért, az OpenMP-ben van egy speciális irányelv a párhuzamos hurok, és a legtöbb cikket szentelt rá.
A cikkben két párhuzamos példát veszünk figyelembe:
- a tömbelemek összegének kiszámítása;
- az integrál számítása a négyszögek módszerével.
A cikk minden példája C ++ -re van írva. A gcc fordítót használtam (de másokat is használhatsz, csak a fordításhoz továbbított kulcsok fognak különböztetni). Az OpenMP támogatása. A gcc-nek el kell fogadnia a -funkciós kapcsolót.
1 A tömbelemek összegének kiszámítása
Mint említettük, az OpenMP lehetővé teszi számunkra, hogy párhuzamosan programozzuk programunkat, de először írhatunk egy szekvenciális programot és kijavíthatjuk, amit csináltunk:
A funkció rendkívül egyszerű, és benne egy hurok, amelynek az iterációját külön szálakra lehet osztani. Ha más könyvtárakat használunk, akkor az iterációt kézi úton kellene elosztani, míg minden egyes szál kiszámítaná az összeg egy részét, és végül a szálak valahogy szinkronizálnák és egyesítenék az eredményeket.
Az OpenMP nekünk is lehetővé teszi, hogy kézzel terjessze a munkát, de gyakrabban, mint amennyire ez nem szükséges, mert sokkal kényelmesebb eszközök vannak.
A harmadik sorban a párhuzamos irányelv párhuzamos területet határoz meg. amely a göndör fogantyú belsejében helyezkedik el. A terület elején létrehoznak szálakat, amelyek számát a num_threads opcióval lehet megadni (a példában a régió két szálon fut).
A stream mindkét helyi változót használhatja. és megosztott. A megosztott változók közösek az összes szálon, nyilvánvalóan nagyon óvatosnak kell lenniük velük (ha legalább egy szál megváltoztatja egy ilyen változó értékét - a többiek várják - az OMP eszközök segítségével megszervezheti). Minden állandót megosztunk - példánkban az "a" és az "n" változók megosztottak.
A szál tartalmazhat egy helyi változókészletet (privát és firstprivate opciók), amelyekhez minden szálon másolatokat készítenek. A privát listában szereplő változók esetében a kezdeti érték nincs definiálva, az elsődleges adathoz - a főfolyamból veszik. A párhuzamos régióban deklarált összes változó helyi (az "i" változó a példánkban).
Opciócsökkentés. egy helyi változót (összeg), valamint egy műveletet, amelyet a helyi változókon végrehajtanak, amikor kilép a párhuzamos régióból ("+"). A helyi változók kezdeti értékét, ebben az esetben a művelet típusa határozza meg (additív műveleteknél - nulla a multiplikatív egységeknél).
A példa ötödik vonala határozza meg a párhuzamos hurok kezdetét. A ciklus Iterációi a megfelelő irányelv alapján a szálak között kerülnek felosztásra.
Az irányelvnek számos lehetősége van, és többet olvashat a vastag tankönyvekben. A hurokban beállíthatja a privát és az első privát beállításokat. de emellett számos új. Például az ütemterv meghatározza, hogyan kell allokálni a szálak közötti iterációt, és a nowait eltávolítja az implicit gát szinkronizálást, amely alapértelmezés szerint a hurok végén van.
A cikk végén egy példány forráskóddal ellátott archívum van csatolva. Ellenőrizheti, hogy a párhuzamos program sokkal gyorsabban fut-e.
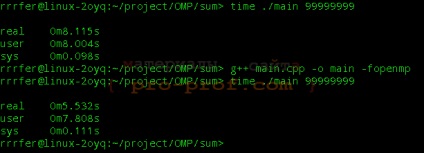
Ábra. 1 OMP párhuzamosság
A tömb elemeinek összegét nagyon gyorsnak tartják, így az ábrán látható eredmények megjelenítéséhez 10-szer kellett elindítanunk a funkciót. A program munkaidejének nagy részét a tömb véletlen számokkal való kitöltésével foglalja el, melyet egy szálon hajtanak végre (ennek következtében az eredmények kissé homályosak). Azonban egy lusta olvasó könnyen párhuzamba állíthatja a tömb kitöltését :) :)
2 Az integrál számítása a négyszögek módszerével
2.1 A négyszögek száma
A cikk a bal oldali téglalapok módszerét használja, amelynek lényege, hogy az integrálható függvény görbéje és az abszcissza tengely közötti tartomány egy meghatározott számú téglalapra van osztva. Minden téglalap esetében a terület számítása történik, a területek összege az eredmény. A "bal oldali téglalapok" kifejezés azt jelenti, hogy minden téglalap bal felső sarkában közvetlenül az integrálható funkció található.
C ++ esetén a leírt algoritmus a következőképpen fejezhető ki (párhuzamos változat azonnal megjelenik, mivel nincs semmi új):
A fenti kódban nincs semmi alapvetően új, csak megjegyezzük, hogy a párhuzamos szakasz leírása nem határozza meg a szálak számát - ebben az esetben az OMP_NUM_THREADS környezeti változó értéke határozza meg. A kód megmagyarázza a négyszögek módját (azok számára, akik elfelejtették), majd megnézzük a módszer végrehajtásának más lehetőségeit. Ezen túlmenően, ezzel az egyszerű példával a négyszögek számának növelésével megvizsgálhatja a pontosság romlását.
Ábra. 2 a pontosság romlása nagy számú téglalappal
Mint érv, a 3. ábrán látható program. 2 a téglalapok számát veszi fel, az x * x függvényt integrálja a [-1, 1] intervallumon. Az integrál pontos értéke 2/3. Minél több téglalap egy meghatározott időközönként - annál kisebbek minden téglalap, ezért a téglalapok "sűrűn csatlakoznak a gráfhoz" és a pontosság növekedni fog. A pontosság valóban megnövekszik, ezt látjuk a téglalapok számának 10-ről 100-ra való növelésére. Nagy pontosságúak viszont pontosan. Az OpenMP nincs ott (megjegyzés: a -fopenmp kulcsot nem használták a fordítás során).
A fenti példában a pontosság esik, mivel a (h) lépés nagyon kicsi értéke a számláló (i) igen nagy értékével megszorozódik. A lépcső alsó soraiban van szemetet, ezt nem lehet elkerülni. Ez a szemetet a szükséges adatok helyett feldolgozzuk. Olyan hibát látunk, amelyet a számítógép nem tud, a program ebben az esetben nem ad kivételeket, különösen nehéz meghatározni az ilyen hibák okait párhuzamos programokban.
Az OpenMP-nek semmi köze ehhez, de kiderül, hogy a munkaszálak száma és a számítási megbízás befolyásolhatja a pontosságot. Az olvasó ezt ellenőrizheti, például az 1 / (x * x) sorozat összegének egymás utáni számításával, amikor x értéke 1 és 100000000 között változik, majd fordított sorrendben. A számítások eredményei eltérőek lesznek, és a számítás fordított sorrendben pontosabb eredményt ad (ha nem világos, miért és ez nagyon érdekes - tudassa velem, egy cikket írok e témában). Az OpenMP nem garantálja a számítások bizonyos sorrendjét, ezért előfordulhat, hogy váratlan hiba jelenik meg, ezt egyes forrásokban többször feltüntetik [2].
2.2 Az integráció pontossága meg van adva
Az előző példában egyik módja szerint egyszerűen párhuzamosan állíthatnánk egymást követő programot (az OpenMP tervezői szerint). Úgy tűnhet, hogy ez mindig így lesz, de nem így van. Alaposan megváltoztatjuk az előző probléma állapotát - most már megadjuk az elérni kívánt pontosságot, és nem a négyszögek számát.
A program fokozatosan megszakítja a lépést, és számolja bele a négyszögek területének összegét, amíg az aktuális és az előző területen lévő teljes terület különbsége kisebb, mint a pontosság. Ezt az ötletet a kódban az alábbiak szerint fejezze ki:
Nyilvánvalóan ez nem a legjobb kód, de megmutatja, hogy az OpenMP bizonyos esetekben (pl. Ez) nem párhuzamosítja a programot. A szálak közötti iterációk kiosztásához az OpenMP-nek képesnek kell lennie arra, hogy meghatározza ezeknek az iterációknak a számát, de ez nem lehetséges a 4. listán.
A külső hurok végrehajtása a meghatározott pontosság eléréséig megtörténik, és nincs mód annak meghatározására, hogy hány iteráció fog történni - ez jobban függ az integrálható funkció tulajdonságaitól, ami lehet.
Úgy tűnik, hogy a belső hurok párhuzamos lehet, de nem az. Az iterációk száma nem határozható meg pontosan, mert mint számlálót, egy frakcionált változót használnak. és ebben hiba is felhalmozódhat (amint azt fent látható). Az OpenMP-ben a párhuzamos huroknak egész számlálóval kell rendelkeznie.
Ez azonban nem jelenti azt, hogy az OpenMP nem tud párhuzamosan megoldani egy ilyen probléma megoldását, de a kódot bizonyos módon meg kell írni. Az a tény, hogy a belső hurok iterációinak száma nem határozható meg, azt jelzi, hogy ez egy rossz kód, függetlenül attól, hogy egymás után vagy párhuzamosan fog működni.
Az OpenMP használatához ebben a példában elegendő előre meghatároznia a belső hurok iterációinak számát, és az egész számlálót használni:
A 4. és 5. listából levont következtetésnek olyannak kell lennie, hogy bár az OpenMP a szekvenciális programok fokozatos párhuzamosításának eszköze, a programot ennek megfelelően meg kell írni. A fent leírt problémák miatt a 5-ös függvény nem feltétlenül működik megfelelően, amikor nagyon nagy pontosságot kér, de erre nem lehet hibáztatni.