Laboratóriumi fizika
A kapilláris átmérőjének mérési eredményeit a 4.2. Táblázat tartalmazza, a 4.3. Táblázatban szereplő további méréseket.
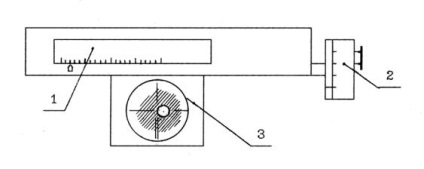
4.5.1 Mérjük meg a kapilláris átmérőjét mikroszkóppal. Ehhez helyezze a kapillárist a mikroszkópos csúszkára. Illessze a szemlencse mikrométerének látóvonalát jobbra, majd a kapilláris nyílás bal széléhez, ahogy a 4.4. Ábrán látható. Vegye ki a mintákat vízszintes léptékben (teljes milliméterben) és egy dobméretben (tized és százmillió milliméter). Keresse meg a kapilláris átmérőjét, mint ezeknek a mintáknak a különbségét. A kapilláris átmérőjét három különböző irányban mérjük. A kapilláris átmérőjénél vegye figyelembe a kapott eredmények számtani átlagát. Számítsd ki a kapilláris R sugarát.
4.5.2 A súlyok felhasználásával határozzuk meg az üres üveg 4 tömegét 0,01 g pontossággal.
4.5.3 A vonalzó segítségével mérje meg a h 'folyadékszint kezdeti magasságát az asztal síkjából.
1 - vízszintes skálán; 2 - dob a dob; 3 - a mikroszkóp látómezeje 4.4 ábra - A kapilláris átmérőjének mérési sémája
4.5.4 Gyorsan engedje le a kapillárist az A pozícióról a B pozícióra (lásd a 4.3. Ábrát), hogy a folyadék a 4 főzőpohárba áramoljon és kapcsolja be a stopperórát.
4.5.5 Mérje meg a kapilláris végének h magasságát a táblázat síkjából.
4.5.6 Ha az üvegben lévő folyadék elégséges (1/2 térfogat), kapcsolja ki a stopperórát, és gyorsan növelje a kapillárst az A pozícióba. Olvassa el a folyadékkiáramlás időtartamát a stopperről.
4.5.7 Mérje meg a h "végső folyadékszintet az 1 edényben.
4.5.8 Határozza meg a főzőpohár tömegét m 2 -vel a folyadékkal.
4.5.9 A 4.3. Táblázatban rögzítsük az értékeket: a gravitációs gyorsulást
(g = 9,8 m / s 2), a folyadék sűrűsége (víz p = 10 3 kg / m 3) és a kapilláris hossza, amelynek értéke a berendezésen van feltüntetve.
5 A Young modulus meghatározása a törzs deformációjában
A munka célja, hogy tanulmányozza a deformált testek viselkedését a külső erők hatása alatt, és kísérletesen meghatározza a Young modulusát a törzs deformációjában.
5.2 Elméleti bevezetés
Az elméleti mechanikában (statika) vizsgálják az abszolút merev test egyensúlyát; Az anyagnak ez az elgondolása elegendő a statisztikai probléma megoldásához - annak meghatározásához, hogy milyen körülmények között lehetséges a testhez alkalmazott erők kölcsönös kiegyensúlyozása. Amikor az anyagok ellenállását ezen erők hatására tanulmányozzák, az anyag tulajdonságainak ilyen durva megközelítő képlete már nem elegendő; figyelembe kell venni, hogy az abszolút szilárd testek nem léteznek természetben.
A valóságban az általuk alkalmazott erők hatása bizonyos mértékig megváltoztatja alakját és méretét, vagyis deformálódnak. A deformációk nagysága és jellege összefügg az általunk használt anyagok szerkezetével és szerkezetével. Mindezek az anyagok két osztályba sorolhatók: kristályos és amorf [1].
A kristályos anyagok nagy mennyiségű kicsi kristályból állnak egymástól. Ismeretes, hogy egy külön kristályban (egykristály) az atomok bizonyos sorrendben vannak elrendezve, kristályrácsot képeznek. A kristályos szerkezet fémekkel rendelkezik (polikristályos testek). Az amorf testekben (üveg, gyanták stb.) A kristályokkal ellentétben nincs szigorú rend az atomok elrendezésében. Csak a legközelebbi szomszédos atomok vannak elrendezve bizonyos sorrendben. De szigorú ismételhetőség minden irányban
és ugyanaz a szerkezeti elem, amely a kristályokra jellemző, nincs amorf test.
Az atomokat az interakció erői egyensúlyban tartják. A testek deformációja az atomok elrendezésének, konvergenciájának vagy eltávolításának változása miatt következik be. A deformáció rugalmas és műanyag. A rugalmas alakváltozások azok a változások, amelyek az elemek alakjában és méretében eltűnnek, miután eltávolították az őket okozó erőket - a test teljesen visszaállítja korábbi alakját. Ezek a deformációk csak az atomok rácsának rugalmas torzítására vonatkoznak. A tapasztalatok azt mutatják, hogy rugalmas alakváltozások figyelhetők meg, míg a külső erők nagysága nem haladja meg a meghatározott határértéket.
Ha a külső erők átlépik ezt a határértéket, akkor az elmozdulás következtében az atomok és a molekulák megváltoztatják "szomszédaikat" és megkezdik a kölcsönhatást
mások. A külső erők megszűnése után már nem térnek vissza korábbi helyzetükre, az elem formája és méretei eredeti formájában nem állíthatók vissza. Az ilyen alakváltozásokat műanyag deformációnak nevezzük. A terhelés eltávolítása után a műanyag deformációi a testben maradnak, ezért maradványként is neveznek. Kristályos anyagokban ezek a deformációk összefüggenek a kristályrács néhány rétegének visszafordíthatatlan elmozdulásával másokkal szemben.
A testre kifejtett erők működésének irányától függően különböző alakváltozatok alakulhatnak ki: feszültség, tömörítés, nyírás, torzió, hajlítás. Meg fogjuk ismerni a legegyszerűbb formák deformációját. Az ilyen testek közé tartoznak az úgynevezett prizmatikus rudak egyenes tengellyel. Emellett azt feltételezzük, hogy a rúdnak nincs tömege.
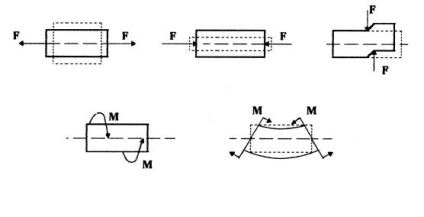
a - nyújtás; b - tömörítés; c - eltolás; r a torzió; d - hajlítás 5.1. ábra - A deformáció típusai
húzó- vagy nyomófeszültség fordulhat elő, ha a külső mentén hatnak egy egyenes vonal (tengelye mentén a rúd) különböző irányokban, amint azt a 5.1 ábra, a, b. Amikor a rúd bőrstimuláló külső erőhatástól egyik a másikhoz képest egy részét, a nyírási alakváltozás lép fel. Így, amint látható az 5.1 ábrán látható, hogy, alkotnak egy pár erő egy kis váll a hosszanti tengelye a rúd sík. Ha a rúd terhelés alatt, hozzon létre ellentétes párjainak az erők merőlegesek a hosszanti tengelye a rúd, a torziós deformáció is fellép, ábrán látható 5,1 g. És végül, ha a két pár ellentétes előjelű erők hatnak a síkban a hosszanti tengelye a rúd, a hajlítási alakváltozás keletkezik, amint azt a 5.1 ábra, d.
A rugalmasság elméjében bebizonyosodik, hogy mindenféle deformáció csökkenthető (feltéve, hogy ezek elég kicsiek) a nyújtás (vagy tömörítés) és a nyírás egyidejű deformációjához.
Az atomok elmozdulása az anyag deformálódása során a külső erők hatására az atomok közötti kölcsönhatás - a vonzási és visszatoloncolási erők - megváltozásával jár együtt. Minden szilárd testben, a külső erők hatására további belső erők merülnek fel,
anyagformálás. Ezek a belső erők ellenállnak a külső erők azon szándékának, hogy elpusztítsák a testet, megváltoztassák formájukat, és elválasszák egymástól az egyiket. Hajlamosak a test deformált része régi alakjának és méretének visszaállítására. Ebből következik, hogy az anyagok ellenállásának problémáinak megoldása érdekében elsősorban a külső erőkből kell tanulnunk, hogy meghatározzuk a belső rugalmas erőket. Ehhez a keresztmetszeti módszert alkalmazzák. amelynek lényege a következő.
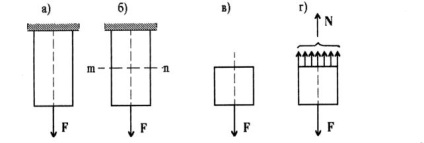
A homogén rúd végét az F keresztmetszeti területre kell alkalmazni, amely egyenletesen működik a rúd egész keresztmetszetén, és a rögzített rúd másik vége az 5.2. Ábrán látható módon a.
Értelmi rúd két részre osztani: egy rész m-n, tengelyére merőlegesen, amint azt a 5.2 ábra, b, és határozza meg az erő, amellyel a részét a rúd aktus egymásra. Mivel mindkét oldalán a rúd egyensúlyban van, akkor a vektor összege ható erők mindegyikük nullának kell lennie. Dobja el a felső és alsó figyelembe az egyensúlyt (lásd. 5.2 ábra c, d). Az egyensúlyi Ennek a résznek nem kell megbontani, ha ő reakciója, hogy - a belső erők helyett
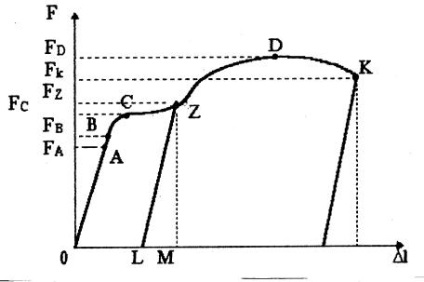
Minden merev test olyan deformációkat ad, amelyek csak egy bizonyos korlátig engedelmeskednek Hooke törvényének. Tekintsük az anyagok viselkedését a szakítóvizsgálatban a megsemmisítésig. A mérések eredményeit a legláthatóbban az úgynevezett nyújtási diagram formájában lehet megjeleníteni. Ha a diagramot a függőleges tengely mentén ábrázoljuk, a terheléseket egy bizonyos skála és a vízszintes skála mentén határozzuk meg - abszolút hosszabbítások. Ha a mintát egy műanyagból (például enyhe acélból) feszítik, a diagram az 5.4 ábrán látható.
Az OA egyenes vonalú rész megfelel a minta rugalmas deformációinak. Az F A koordinátája a P szakasza arányának megfelelő húzóerő értéke, vagyis a legnagyobb feszültség, amelynek feleslege eltér a Hooke-törvénytől.
Amint a húzóerőt az FA érték fölé emelték, a deformáció gyorsabban növekszik, mint a terhelés - a diagram görbe vonalú, konvexitással felfelé. Azonban a B pont előtt a deformációk rugalmasak, vagyis a minta visszanyeri alakját a terhelés eltávolítása után. A B ponton túl rugalmas deformációk jelentkeznek.
A stressz, amikor meghaladja a test deformálódását, az σ y rugalmassági határ; a diagramban a feszültséget okozó terhelést az F B koordinátával mérik.
Az A és B pontok olyan közel vannak egymáshoz, hogy általában az elasztikus határt és az arányossági korlátot tekintik egyenlőnek. Ezért gyakran mondják, hogy az anyag követi Hooke törvényét, amíg el nem éri a rugalmassági korlátot, bár helyesebb lenne mondani - az arányosság határértékét.
5.4 ábra - Enyhe acél húzása
Az F húzóerő bizonyos értékénél az anyag "áramlik"; A deformáció növelése érdekében szinte felesleges a húzóerő növelése. Az ábra vízszintes (vagy majdnem vízszintes) platformot képez.
Az ilyen anyagáramlást okozó feszültség - a deformáció növekedése állandó (megközelítőleg) terhelésnél - σ m termelési pontnak nevezzük.
Az öntési pont létrejötte után az anyag ismét elkezd ellenállni a további nyújtásnak, és növelni a nyúlást, meg kell növelni az erőt. A diagram D pontja megfelel a terhelés legnagyobb értékének.
Ha a terhelést egy olyan pontban leírt állapotban távolítjuk el, amely a C és D pontok között fekszik, akkor a diagram kirakodásakor egy egyenes vonallal jelenik meg, amely megközelítőleg párhuzamos az OA egyenes vonalával. Így a minta ebben az esetben nem tér vissza eredeti méretéhez; az LM szegmens rugalmas nyúlást jelent, amely még mindig változik a terhelés arányában az elasztikus rugalmassági modulussal; szegmens OL - maradék nyúlás és szegmens OM teljes megnyúlás F z terhelésnél.
A húzóerőt legnagyobb értékét az FD ordinátán ábrázoljuk; gyakran destruktív terhelésnek nevezik. mivel neob-