Diszkrét elemzés
Az egyenértékűségi osztályok
Tétel. Tegyük fel, hogy A adódik, és U egyenértékűségi viszony az A × A-ra
Ua = b | (a, b) Az U> -ről
formák (az egybeeső egységek eltávolítása után) az A halmaz partícióját.
Bizonyítás. Először is, azt bizonyítjuk, hogy ha az Ua és az Ub összefonódik, akkor azok egybeesnek. Valóban, ha b U Ua. (a, b) U U. Az U (U, U) és (b, c) U U (a, b) U reláció átvitelessége azt jelenti, hogy (u, c) U U, tehát Ua ⊂ Ub.
Az összefüggés szimmetriája miatt van egy 0 Ub is. ahonnan Ub ⊂ Ua. és ezért ezek a készletek egyenlőek.
Mindegyik alcsoport nyilvánvalóan nem szabad - ezt bizonyos elemek határozzák meg, amelyek belépnek. A készlet minden egyes eleme (szintén nyilvánvalóan) egy ilyen alcsoporthoz tartozik, tehát van egy partíciónk.
A tételben tárgyalt alcsoportokat egyenértékűségi osztályoknak nevezzük. Hamarosan szükségünk lesz rájuk.
Tegyük fel, hogy kaptunk egy U-kapcsolatot definiált U-t. Gyakran szükséges a tranzitíven bezárni: nagyobb arányú TU-t létrehozni. amely tranzitív és ugyanakkor a legkisebb az összes tranzitív kapcsolat között.
TU: = U;
az i számára A do
a j-ról A do
k számára A A-t
ha (j, i) A TU ∧ (i, k) -ról TU-ra
TU: = TU ∪
fi
od
od
od
Itt od a záró konzol. és fi a zárójel az if számára.
Az algoritmus egy kezdeti hozzárendelést és egy primitív hármas ciklust tartalmaz i, j, k változókkal. amelyben, ha van pár (j, i) és (i, k) a relációban. akkor a páros (j, k) is benne van.
A trükk az, hogy az algoritmus csak akkor működik megfelelően, ha a "köztes index" i ciklusa külső. Az algoritmusra később visszatérünk. Célszerű lenne egy pillanatra megfontolni a fejlődését.
Az A. sorozatban megadott U. antiszimmetrikus átmeneti reláció határozza meg a részleges sorrendet ezen a készleten. Köszönjük, hogy elemeket hasonlíthatunk össze egymással, de nem minden elem hasonlítható össze.
Amikor részleges sorrendet adunk meg, ha egy elempár (a, b) U-hoz tartozik, akkor azt mondjuk, hogy a megelőzi b. Ha e két elem közül egyik sem előzi meg a másikat, azt mondják, hogy nem hasonlíthatóak össze.
Az antiszimmetrikus állapot itt szükséges ahhoz, hogy kizárjuk az egyenértékű elemek lehetőségét. A láncok kialakításához szükséges a tranzitivitási feltétel.

Wilfredo Pareto (1848-1923) olasz közgazdász azt javasolta, hogy e feladatokban egy tervet használjanak, melyet tiszteletére Pareto határnak neveznek. Most leírjuk.
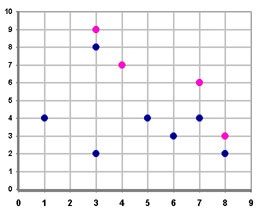
Az ábrán az A készlet merészen rajzolt pontokat tartalmaz a síkban. Egy pont előzi meg a másikt, ha mindkét koordinátája nem kisebb, mint a másik megfelelő koordinátái, és legalább egy koordinátája szigorúan nagyobb. Ebben az esetben a Pareto határa vörösre festett pontokból áll.
A több helyi kapcsolatokat széles körben használják az adatbázisok egyikében.
A relációs adatbázisban található információk táblákban vannak tárolva. és minden táblát egy bizonyos többüléses kapcsolatként kezelnek. Például vegyük be a hallgatói csoport regisztrációs kártyájának egy részét (ezeket a dekáni iroda hallgatói osztályán használják)
Ennek a táblázatnak a sorai (a sort sorszámot nem soroljuk fel) öt elemből álló csoportnak tekinthető: (Név, Szám, Mégse, Mégse2, Mégse3). és ezért az öt SFIO × N × M1 × M2 × M3 sorozatú Descartes termék elemeként.
Így minden ilyen táblázat tekinthető öt helyre.
A relációs adatbázisokban az információt táblák és kapcsolatok sorozata határozza meg, és az információra és az ahhoz kapcsolódó követelményekre vonatkozó összes műveletet e táblázatokban ismertetjük.