Az algoritmus finomsága
Elágazás (a G készlet részekre bontása). Megálltunk
8. Az algoritmus finomsága. Az algoritmus végességének a G készlet végességéből következik.
A fióktelepek és határok módszerével olyan problémát megoldó algoritmust értünk, amely fa-szerű struktúrával rendelkezik az optimális megoldás megtalálásához és a becsült problémák megoldásának eredményeihez. A fa struktúrát általában ágfának nevezik.
Az ágak és határok algoritmusának hatékonyságát a megoldott problémák száma határozza meg. A probléma megoldása két fő szakaszból áll. Az első szakaszban az optimális megoldás (vagy közel áll hozzá). A második lépés bizonyítja a kapott oldat optimumát. A második szakasz, mint általában, több munkaigényes, mint az első. Ez azt jelenti, hogy az optimális érték elérése előtt megoldható részfeladatok száma lényegesen kisebb lehet, mint az alproblémák száma, amelyek megoldhatók az optimitás bizonyítására.
2. Az utazási ügynök problémája
A klasszikus utazási ügynök problémát (ZK) a következőképpen fogalmaztuk meg: van egy teljes súlyozott orientált grafikon G hurok nélkül, ahol a csúcspont N =; minden ív súlya nem negatív; ebben a gráfban meg kell találni a minimális súly Hamilton-ciklusát.
A ZK-ra vonatkozó kezdeti információkat a nxn méretű mátrixnak kell tekinteni. S =, ahol sij a görbe γ (i, j) súlya, i =. j =. i ≠ j; az S mátrix fő átlójának elemei nullák.
Egy tipikus értelmezésben a G gráf 1., 2., ..., n csúcsai városok. Az ívek lehetséges elemi átmeneteket jelentenek. Eladó, eredetileg található 1, meg kell, hogy az egész város többi része, látogatás mindegyik pontosan egyszer, majd visszatér a városba 1. A súlyokat az íveket a grafikon értelmezi a hossza a megfelelő elemi átmenetek. Meg kell találni a megengedett (azaz a kiszabott követelményeknek való megfelelés) utazási utat minimális utazási hosszát. Figyelembe véve más lehetséges értelmezéseket, az S mátrixra nem vonatkozik a szimmetria követelménye, és a háromszög egyenlőtlenség nem tekinthető kötelezőnek.
3. Az utazási ügynök problémája dinamikus programozási módszerrel
Az ágak és határok módszerével olyan problémát megoldó algoritmust értünk, amely fa-szerű struktúrával rendelkezik az optimális megoldás megtalálásához és az értékelési problémák megoldásának eredményeinek felhasználásával. A fa struktúrát általában ágfának nevezik.
A ZK megoldásának egyik fő algoritmusa a dinamikus programozás elve. Az algoritmus bemutatásakor ragaszkodni fogunk a probléma adott tipikus értelmezésének megfelelő terminológiához.
Legyen önkényes város (pl # 206; N), és V olyan városok részhalmaza, amelyek nem tartalmazzák a várost 1 és a várost. Legyen M (i, V) halmaza utak, amelyek mindegyike kezdődik i, befejeződött 1 és kiterjeszti kizárólag közbenső keresztül városok meghatározott V, bemegy mindegyik pontosan egyszer. B (i, V) jelöli az M (i, V) készlet legrövidebb útjának hosszát. A probléma megoldása esetén a B (i, V) a Bellman függvény. Nyilvánvaló, hogy a B (1,) a minimális hossza egy egyszerű (öncsomópont nélküli) zárt útvonalnak, amely minden városon áthalad.
Ha V egy singleton-készlet, V =, ahol j ≠ 1 és j ≠ i, akkor az M (i, V) halmaz egy egyenesből áll μ = (i, j, 1). ezért
én # 206; N, j # 206; , j ≠ i. (1.1)
Tegyük fel, hogy a B (i, V) függvény értékei minden i # 206; N \ és minden lehetséges k-elem (k Az (1.1) - (1.12) egyenletek a dinamikus programozás visszatérési viszonyai az utazási ügynök problémájának megoldásához, az inverz Bellman-módszer megvalósítását szolgálják. A probléma számítási komplexitása egyenlő, ahol C egy tetszőleges konstans (C> 0), n a városok száma. Példa 1.1 Megoldani az utazási ügynök problémáját, amelyet a mátrix határoz meg: Először az (1.1) képlet segítségével meghatározzuk a B (i,): A (2) -ben = 5 + 6 = 11; A (3) = 2 + 2 = 4; A (4) = 5 + 2 = 7; A (2) -ben = 2 + 1 = 3; A (3) = 1 + 1 = 2; A (4) -ben = 4 + 6 = 10. Továbbá, az 1.2. Pont szerint egymás után (az alábbi egyenletek bal oldalánál a j paraméter értékeit választjuk ki, amelyen az (1.2) jobb oldalán lévő minimális érték valósul meg: In (2,) = min [s23 + B (3,); s24 + B (4,)] = min (5 + 2; 2 + 10) = 7; A (3) -ben = min [s32 + B (2,<4>); s34 + B (4,<2>)] = min (2 + 3; 1 + 7) = 5; A (4) = min [s42 + B (2,<3>); s43 + B (3,<2>)] = min (5 + 11; 4 + 4) = 8; = min (4 + 7; 3 + 5; 4 + 8) = 8. Tehát a vizsgált példában a kritérium optimális értéke 8. A végrehajtott kiválasztás lehetővé teszi az optimális útvonal meghatározását. Ez a következő: A közvetlen Bellman-módszerrel kapcsolatos kapcsolatok feljegyzése érdekében új bejegyzést vezetünk be. Legyen M „(V, i) - meghatározott utak, amelyek mindegyike kezdődik 1 menetben köztitermékekként csak a város részhalmaza V, bemegy mindegyik pontosan egyszer és végződik, i; itt, mint korábban, i önkényes város (i # 206; N), és V az N részhalmaza, amely nem tartalmaz városokat 1 és i. Az M '(V, i) készlet legrövidebb útjának hosszát B * (V, i) jelöli. Nyilvánvaló, hogy a B * (, 1) az összes városban áthaladó egyszerű (öncsomópont nélküli) zárt útvonal minimális hossza. Ha V egy singleton-készlet, V =, ahol j ≠ 1 és j ≠ i. akkor az M '(V, i) halmaz a μ = (1, j, i) egyedi útból áll. ezért Tegyük fel, hogy a B * (V, i) függvény értékei minden i # 206; N és minden lehetséges k-elem (k Az egyenletek (1.3) - (1.4) a dinamikus programozás ismétlődő kapcsolatai a klasszikus utazási ügynök problémájának megoldására, a közvetlen Bellman-módszer megvalósítását szolgálják. 1.2. Példa A közvetlen számolási módszer segítségével oldja meg a mátrix által meghatározott utazási ügynök problémát: (vegye figyelembe, hogy az S mátrix ebben a példában ugyanaz, mint az előzőben). Először az (1.3) képlet segítségével meghatározzuk a B * (, i) értékét: B * (, 3) = 4 + 5 = 9; B * (, 2) = 3 + 2 = 5; B * (, 2) = 4 + 5 = 9; B * (, 4) = 4 + 2 = 6; B * (, 4) = 3 + 1 = 4; B * (, 3) = 4 + 4 = 8. Továbbá az (1.4) képlet szerint egymás után (az alábbiakban felsorolt egyenletek mindegyikének bal oldalán a j paraméter azon értékei kerülnek kiválasztásra, amelyeken az (1.4) jobb oldalán található minimális érték valósul meg: B * (, 4) = min [B * (, 3) + s34; B * (, 2) + s24] = min (9 + 1; 5 + 2) = 7; B * (, 3) = min [B * (, 4) + s43; B * (, 2) + s23] = min (6 + 4; 9 + 5) = 10; B * (, 2>) = min [B * (, 4) + s42; B * (, 3) + s32] = min (4 + 5; 8 + 2) = 9; Tehát a vizsgált példában a kritérium optimális értéke 8. A végrehajtott kiválasztás lehetővé teszi az optimális útvonal meghatározását. Ez a következő: Egy másik algoritmus az utazási ügynök problémájának megoldására az ágak és határok módszere. Lényegében ez a megoldások teljes körű keresésének néhány módosítása, melyet optimalizálnak az a tény, hogy bizonyos kritériumok szerint a nem optimális keresési készleteket levágják. Formálisan egy variáns fa alkotja a gyökérből kiindulva. A gyökérben felső és alsó határértéket kell megadni. Aztán elágazunk. Minél kisebb lesz a fa töredéke, annál sikeresebb az ág és a határmód. A következő fogalommeghatározások tartják: A jelenlegi rekord a végrehajtási folyamat során elért alacsonyabb becslések közül a legnagyobb. A csúcsot halottnak hívják, ha a legmagasabb pontszám nem haladja meg az aktuális rekordot. Hasznos a további elágazások elvégzése. A terminál olyan csúcs, amelyben a felső és az alsó határ egybeesik. A már elágazó csúcsot zártnak hívják. A csúcsok, amelyek nem halottak, sem terminálok, sem zártak, nyitottak. További elágazást végeznek bennük. A megoldás akkor fejeződik be, ha nincs opciójuk fa csúcspontja. A legjobb megoldás a jelenlegi rekord. A felső határt a "mohó" algoritmus segítségével határoztuk meg. A mohó algoritmus olyan algoritmus, amely a legrövidebb távolság megtalálásához a legrövidebb, még nem választott szélhatárt választja, feltéve, hogy nem képezi a hurokat a már kiválasztott szélekkel. "Greedy": ez az algoritmus azért nevezhető el, mert az utolsó lépésekben brutálisan kell fizetni a kapzsiságért (az utolsó borda rendszerint a legnagyobb vagy ahhoz közeli). Stratégia: "Menj a legközelebbi (még nem bejövő) városba." Vegyük például a 2. ábrán látható hálózatot. 2, ami keskeny rombusz. Engedje el az utazó ügyintézőt a városból 1. Az algoritmus "megy a legközelebbi várost" veszi a városba 2, majd 3, majd 4; az utolsó lépésben meg kell fizetnie a kapzsiságért, és vissza kell térnie a rombusz hosszú átlója mentén. Ennek eredményeként nem lesz a legrövidebb, de a leghosszabb túra. Az alsó kötés kiszámításához először összegezzük a minimális elemeket sorok és oszlopok szerint, majd válasszuk ki a legnagyobb összegeket, de figyelembe kell venni a konfliktust. 2.1. Példa Az ágak és határok módszerével oldja meg az utazási ügynök problémáját, amelyet a mátrix határoz meg:
4. A kereskedő problémája a fióktelep és a határoló módszer szerint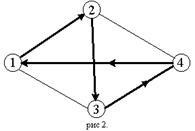

1. A gyökér felső és alsó határát kiszámítjuk:
A felső becslés az úgynevezett "mohó" algoritmus segítségével történik: minden átmenet az aktuálistól a legközelebbi városig történik. Keresse meg az útvonalat:
1 ® 2 ® 4 ® 3 ® 5 ® 1
Ennek az útvonalnak a teljes költsége 12, meghatározza a gyökér legmagasabb becslését.
Az alsó határ kiszámításához először összegezzük a minimális elemeket sorok és oszlopok szerint, majd a kapott összegek közül válasszuk ki a legnagyobbat:
A sorokban: 2 + 1 + 2 + 2 + 2 = 9
Oszlopok: 2 + 2 + 3 + 1 + 2 = 10
Válassza ki az értékek maximális értékét, és válassza a 10 lehetőséget.
Elemezzük az oszlopokat: 2-re (konfliktus) léphetünk. Ezért az alsó határ 10 + 2 = 12.
A probléma megoldása következtében nem kell tovább határoznunk. Meg fogjuk írni az optimális útvonalat az utazó ügynöknek:
Így a probléma megoldódott.
A gyakorlat egyre több és több optimalizációs problémát generál, összetettsége pedig növekszik. Új matematikai modellek és módszerek szükségesek, amelyek figyelembe veszik számos kritérium létezését, és globális keresést végeznek az optimumon. Más szóval az élet arra kényszerít bennünket, hogy kifejlesszük az optimalizálás matematikai berendezéseit.
A diszkrét optimalizálás valós alkalmazása nagyon összetett. A modern módszerek optimalizálása nem mindig képes megoldani az emberi segítség nélküli valódi problémák megoldását. Nem, mindaddig, amíg van olyan elmélet, amely figyelembe veszi a probléma megfogalmazását leíró funkciók bármely jellemzőjét. Előnyben kell részesíteni azokat a módszereket, amelyek könnyebben kezelhetők a probléma megoldásában.
Az alkalmazott források listája
1. Bellman, R. Dinamikus programozás - M. IL, 1960.- 400 p.
2. Bellman, R. A dinamikus programozás során alkalmazott problémák - M. Nauka, 1965. - 457 p.
4. R. Bellman, S. Dreyfus A dinamikus programozás alkalmazásával kapcsolatos problémák - M. 1965 460 p.
Elágazás (a G készlet részekre bontása). Megálltunk
Információ a munkáról "A programozás módja és a fiókrendszerek a diszkrét optimalizálási problémák megoldási folyamataiban"