Leíró geometria

Kezdőlap | Rólunk | visszacsatolás
1. Közép vetületek és alapvető tulajdonságaik.
Ha a központi vetület (a központi vetületek kialakítása) a vetületek síkját és a vetületek középpontját adja - olyan pont, amely nem fekszik a vetületek síkjában. Az 1.1. Ábrán a P sík a vetületek síkja, az S pont a vetületek középpontja.
Ha tetszőleges pontot vetít ki rajta és a vetületek középpontját, rajzoljon egyenes vonalat. Ennek a vonalnak a metszéspontja a vetületek síkjával az adott pont központi vetülete az előre jelzett síkban.
Az 1.1. Ábrán az A pont központi vetülete az SA vonal kereszteződésének a pontja a P. síkkal. A pp síkra vonatkozó bp, cp, dp pontok B, C, D középpontjait is felépítik.
A vetületek és a vetített pontok középpontján áthaladó egyenes vonalakat kiálló vonalaknak nevezik.
A két különböző B és C pont bp és cp középpontjai, amelyek egyetlen vetítővonalon helyezkednek el, egybeesnek. Az egyik vetületi vonalhoz tartozó helyek mindegyike egy vetületi központban egy adott vetületi síkon egy központi vetületet tartalmaz.
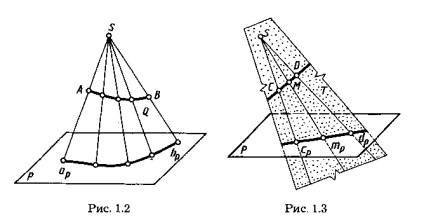
Annak érdekében, hogy a reverzibilis rajz, t. E. Egy egyértelmű meghatározása pont helyzetét a térben annak előrejelzések, szükségünk van további feltételeket, például beállíthatja a központ a második vetítés. A középső vetületeknél bármely vonal vagy felület kivetítése minden pontjának vetületeként összeállítható (lásd az 1.2., 1.3. Ábrákat). Ebben a kiálló vonalak (teljes egészében) van átvezetve, minden pont egy görbe vonal képez vetített kúpos felület (ábra. 1.2), vagy lehet egy síkban (lásd. Ábra. 1.3), amely az úgynevezett kiálló.
A vonal görbületének vetülete a kinyúló kúpos felület metszéspontja a vetületek síkjával. Így, az 1.2 ábrán a kiálló kúpos poverhnostQ metszi a P sík az előrejelzések apbp görbe, amely kiálló vonallal AV.Odnako vetítési vonalak nem azonosítja a tervezett vonal, mivel a kiálló felület lehet végtelen számú vonalak kiálló ugyanabban a sorban a síkban előrejelzések (1.4 ábra).
Amikor egy egyenes vonalat mutat, amely nem haladja meg a vetületek középpontját, a kiálló felület a sík. Így, az 1.3 ábrán a kiálló síkban T által alkotott vetített vonalak SC és SD, áthaladó C és D pontok egy egyenes vonal, metszi a P sík az előrejelzéseket az előre cpdp, amely a nyúlvány a vonal CD. Ennek megfelelően a közvetlen CD M pontjának vetülete a cpdp vetülethez tartozik.
A vonalak, felületek vagy testek előrejelzéseinek elkészítéséhez gyakran elegendő csak bizonyos jellemző pontok előrejelzéseinek kialakítása. Például, amikor az ABC háromszög projekciójának (1.5. Ábra) vetületeinek kirajzolását a vetület síkjára tervezzük, elegendő az A, B, C csúcspontok ap, bp, cp vetületeinek elkészítése.
A központi vetület tulajdonságai.
1. Központi vetítéssel:
a) a pont egy pontra vetül;
b) az egyenes vonalat, amely nem halad át a vetületek középpontján, egy egyenes vonalra vetül ki (egy egyenes vonalat mutat ki);
c) egy lapos (kétdimenziós) minta nem tartozó kiálló sík előrejelzések formájában kétdimenziós alakzatok (alakzatok tartozó kiálló síkra vetített vele együtt formájában egy egyenes vonal);
d) a háromdimenziós alak kétdimenziós alakban jelenik meg.
2. A számok központi vetületei megtartják kölcsönös függőségüket, folytonosságukat és más geometriai tulajdonságokat.
3. Egy adott vetületi vetület esetén a párhuzamos síkok ábrái hasonlóak.
4. A középső vetítés egy-egy egyezést hoz létre az ábra és a kép között, például filmnézetben, filmben megjelenő képek.
A középső előrejelzések perspektivikus tárgyak ábrázolására szolgálnak. A középső vetületek képei tisztaek, de a műszaki rajzolás kényelmetlen, mivel a metrikat nem tartják be.
2. Párhuzamos vetületek és alapvető tulajdonságaik.
A párhuzamos vetület (1.6. Ábra) a központi vetület speciális esetének tekinthető, amelyben a vetületek középpontja végtelenre (Soo) kerül. Párhuzamos vetítés esetén párhuzamos vetületeket használnak, amelyeket adott irányba húznak a vetületek síkjához képest. Ha a vetítési irányt merőleges vetülete síkra, az úgynevezett vetülete, téglalap vagy ortogonális, más sluchayah- ferde (ábra. 1.6 vetítési irányt nyíl jelzi szögben nem 90 ° -kal egyenlő, hogy a P sík a nyúlványok).
Párhuzamos vetület esetén a központi vetület összes tulajdonsága megmarad, és a következő új tulajdonságok fordulnak elő.
1. A párhuzamos vonalak párhuzamos vetületei párhuzamosak, és az ilyen vonalak szegmensek hossza aránya megegyezik a vetületük hosszának arányával.
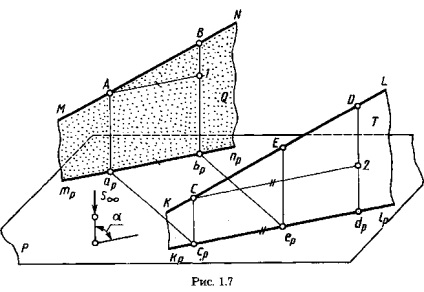
Ha az MN és KL vonalak (1.7. Ábra) párhuzamosak, akkor a Q és T vetületi síkok párhuzamosak, mivel az egymást keresztező vonalak kölcsönösen párhuzamosak: MN || Hipotézis szerint Aar || Csp || S. Következésképpen az mp np és kp lp vetületek párhuzamosak, mint a Q és T párhuzamos síkok metszésvonalai a P. síkkal.
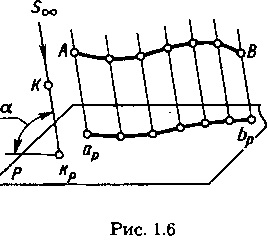
Egy tetszőleges AB szegmenst jelölünk az MN vonalon és egy tetszőleges szegmens CD-t a KL vonalon. Az A-1 vonallal a Q-A síkba rajzolunk. || és a T síkban a C ponton keresztül az egyenes vonalat
C-2 || cpdp. A szegmensek [A-1] = [apbp], [C-2] = [Cpdp] a párhuzamos párhuzamos szegmensek között. A C-2 szegmensei || c, dP || appp és következésképpen a C-2 || A- 1. A B-1 szegmensek || D-2 || S, AB-1 háromszög
háromszög CD-2, mivel minden oldaluk kölcsönösen párhuzamos. Az AB-1 és CD-2 háromszögek hasonlóságából következik:
A következőkből következik:
a) ha egy vonalszakasz hossza bizonyos fokig meg van osztva, akkor a szegmens vetületének hossza e pont vetületével azonos arányban oszlik (1.8. ábra):
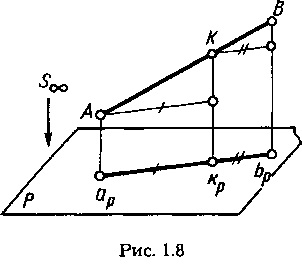
b) a kölcsönösen párhuzamos vonalak egyenlő hosszúságú vetületei egymással párhuzamosak és egyenlő hosszúságúak.
Ez nyilvánvaló, mivel az AB |: | CD | = 1 az apbp | lesz = | cp dp |. Ezért általános esetben ferde vetítéssel párhuzamogram, rombusz, téglalap, négyzet párhuzamos ábrázolásra kerül.
2. A vetületek síkjával párhuzamos sík-ábrázolást ezzel a síkkal párhuzamos vetítéssel vetítjük ki.
3. Egy kép párhuzamos átadása a vetületek síkjában vagy síkjában nem változtatja meg az ábrázolás alakját és méretét.
A párhuzamos vetületek, mint a központi egységek ugyanabban a vetületi központban, nem biztosítják a rajz visszafordíthatóságát. Egy pont és egy vonal párhuzamos vetületeinek technikáival párhuzamos felszínt és testet lehet előállítani. A párhuzamos vetületek különböző technikai eszközök vizuális képeinek és részleteinek, például az axonometrikus vetületek megalkotására szolgálnak, amelyeket alább tárgyalunk.
2. Négyszögletes (merőleges) vetület.
A párhuzamos vetület speciális esetét, amelyben a vetületi irány merőleges a vetületi síkra, négyszögletes vagy ortogonális vetületnek nevezik. Egy pont téglalap alakú (ortogonális) vetülete egy merőleges alap, amely a pontoktól az előrejelzések síkjáig húzódik. A D pont négyszögletes vetülete dp az 1.9. Ábrán látható.
A párhuzamos (ferde) vetületek tulajdonságai mellett az ortogonális vetület a következő tulajdonsággal rendelkezik:
Két egymásra merőleges egyenes vonalának merőleges vetületei, amelyek közül az egyik párhuzamos a vetületek síkjával, a másik pedig nem merőleges rá, egymásra merőlegesek.
Bizonyítsuk be ezt. Az 1.10. Ábrán az ABC = 90 ° szög; (AB) || P; (CB) nem merőleges a P-re. Megmutatjuk, hogy a szög arbp = 90 °.
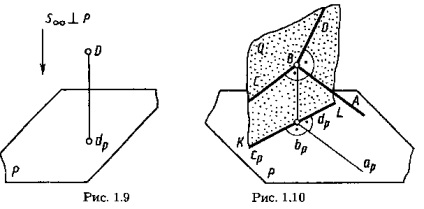
Ennek megfelelően, DBA = 90 ° szög esetén (DB) nem merőleges a P és (AB) || P van:
Az ortográfiai vetület több előnnyel rendelkezik a központi és a ferde párhuzamos vetületnél. Számukra elsõsorban a pontok ortogonális vetületeinek geometriai konstrukcióinak egyszerûsége és az alakzatok bizonyos körülményei között a vetületek alatt kialakuló megõrzés, valamint a tervezett figurák mérete.
Ezek az előnyök biztosítottak ortogonális kivetítést a rajzok kidolgozásához minden iparágban és az építőiparban.
3. A vetület három egymásra merőleges vetületre vetül.
A rajz visszafordíthatósága úgy nyújtható, hogy két nem párhuzamos vetítési síkot vet fel.
A kivetítés kényelmét tekintve két egymásra merőleges síkot választunk két vetületi síknak (1.11. Ábra). Az egyiket általában vízszintesen helyezzük el - a vetületek vízszintes síkját, a másik pedig függőlegesen. A függőleges síkot a vetületek elülső síkjának nevezik. Ezek a vetületi síkok metszi a vetület tengelyét.
A vetítési tengely két vetületi síkot két fél síkra osztja.
Jelölje ki a vetítés síkját betűkkel: V - elülső, H - vízszintes, vetítési tengely - az x betű vagy az alakban
frakciók V / H. A síkok V és V H alkotják a rendszert, N. (Amellett, hogy ezek a vetítési síkok használt megnevezések az irodalomban és más elnevezések például írni π indexek).
A vetületi síkok, amelyek metszenek egymással, négy dihedral szöget alkotnak, amelyek közül az 1.11. Ábrán bemutatott (az V, H arcok jelölésével) az elsőt tekintjük.
A rajzokon sok részletet ipar működik is egy olyan rendszer két egymásra merőleges síktól metsző a függőleges tengelyen z a nyúlványok (ábra. 1.12). Ebben a frontális vetítési síkban marad, mint sík V, és erre merőleges, és jelöljük W úgynevezett profil vetítési síkban.
Két egymásra merőleges vetületi sík rendszerében egy pont vízszintes vetülete egy pont téglalap alakú vetülete a vetületek vízszintes síkján;
A pont elülső vetülete egy pont téglalap alakú vetülete az elülső síkban.
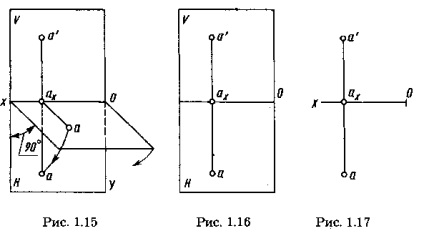
A V, H rendszerben az A tetszőleges A pont kivetítéseinek kialakításának vizuális ábrázolása az 1.13. Ábrán látható. Az a-val jelölt vízszintes vetületet az A ponttól a H síkhoz húzódó merőleges metszéspontjával találjuk meg ezzel a síkkal. Az "A" ponttól az "A" pontig húzódó merőleges metszéspontjával ez a sík található.
A V és H síkokra merőleges Aa 'és Aa nyílások a Q síkhoz tartoznak. A merőleges a vetületek síkjára, és metszi a pontok tengelyén a vetületek tengelyét. Három egymásra merőleges Q, V és H sík metszi kölcsönösen egymásra merőleges vonalak mentén, azaz egyenes vonalakat. Az aax és az x tengely egymásra merõleges.
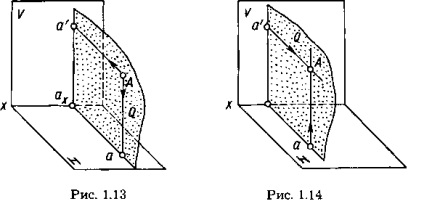
Így két pont téglalap alakú kivetítése teljesen meghatározza a térbeli helyzetét a kölcsönösen merőleges vetületi síkok egy adott rendszeréhez képest.
A következőkben a pontok metszetleges vetületének egy pontjának téglalap alakú projekcióit egy pont ortogonális vetületének nevezzük.