Az Euler-egyenlet a fizikában
Az Euler-egyenlet a hidrodinamikai egyenlet, amely leírja az ideális folyadékáramlás áramlását, és figyelembe veszi a folyadékra ható erőket.
Az Euler-modellben ideális folyadékot kell figyelembe venni, amelyben nincs hővezetőképesség (a folyadéknak állandó hőmérséklete van, nem melegszik fel és nem hűl), és viszkozitása (nincsenek súrlódási erők a folyadékban). Ezért az ilyen folyadékra ható erők a saját tömegük, a gravitációs és a tehetetlenségi erők nyomásának hatáserősségére redukálódnak.
Az Euler-egyenlet vektoros formában
Vektoros formában az Euler-egyenletnek a következő formája van:
A jobb oldalon található kifejezések figyelembe veszik a külső erők és a test saját tömegének nyomását: - a külső erőerő erőssége, - a folyadék nyomása, - a folyadék sűrűsége. A vektor a folyadék sebessége. - Jelentős származék, amely mozgó pont gyorsítása egy anyagi közegben. A lényeges származék részleges származékokká bomlik. majd az Euler-egyenlet a következő alakú:
Az utóbbi egyenletet Gcmeko formájú gátló folyadék mozgásának egyenletének is nevezik. Szintén alkalmas arra, hogy elválasztja a mozgás örvényösszetevőjét egy kifejezés formájában, és a részleges származék az időhöz képest tükrözi a helyi gyorsulást, amely az instabil áramlásokra jellemző.
Az Euler-egyenlet megoldása
A számításokban célszerűbb az Euler-egyenletet skaláris formában használni:
ahol a sebesség és a külső erők vektorai, valamint a nyomásmező bontásra kerülnek a koordináta-tengelyekhez képest.
A hidrodinamika és a gázdinamika egyszerűen alkalmazott problémáinak megoldásakor időnként elegendő figyelembe venni az egyensúlyi állapotú egydimenziós áramlást. Ebben az esetben az Euler egyenlet egy egyszerű formát ölt:
Ennek a kifejezésnek a beépítésével meg tudjuk szerezni a Bernoulli-egyenletet:
Euler mögöttes hidrodinamikában használják különböző területeken: a design repülőgépek és hajók, a számítás turbinák, szivattyúk és csővezetékek, a tanulmány óceáni áramlatok és a mozgás a felszín alatti vizek.
Példák a problémamegoldásra
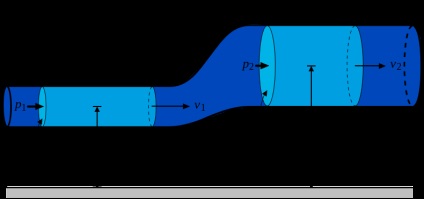
A vízszintes csövön átfolyó 950 kg / m3 sűrűségű folyadék áramlik át, a cső bemeneti nyomása 0,3 MPa, a cső kiáramlása esetén 1 MPa. A cső bejáratának sebessége 50 m / s. Határozza meg a cső kimeneti sebességét.
Egy Euler egyenletet írunk le egy álló, egydimenziós áramlásnak:
Mindkét oldalt dx-vel szorozzuk és integráljuk:
Ezt a kifejezést a bemeneti és kimeneti szakaszokra írjuk: