Prizma anyag törésmutatójának meghatározása goniomerrel
Cél: megvizsgálni a prizma anyag törésmutatójának függését az incidens fény hullámhosszán.
Eszközök és tartozékok: G-5 goniométer, prizma, fényforrás.
A fénytörés egyik törvénye szerint az anyag törésmutatója állandó érték. Ezt a törvényt arra használták fel, hogy megoldják a különböző optikai eszközök fénysugarának útjának építésével kapcsolatos gyakorlati problémákat. A problémák megoldásakor nem volt szükség annak meghatározására, hogy egy monokromatikus (egyszínű) sugárral foglalkozunk, vagy az incidens fény összetett összetételű, és különböző hosszúságú hullámokat tartalmaz.
Meg kell jegyezni, azonban, hogy amikor a fehér fény áthalad a háromszög prizmához a gerenda, elbontjuk alkotórészeire, amely a folytonos spektrum (1. ábra). Ezért a különbözõ hullámhosszú fényeket ugyanabban az anyagban különbözõ módon torzítják. Ezt a jelenséget az okozza kábítószerfüggőség a törésmutatója az optikai hullámhosszú, az úgynevezett diszperziós fény, így a refraktív rezultatedvukratnogo prizmoyspektr nevezzük diszperziós spektrum.
A fény diszperziója az elektromágneses elmélet és az anyag elektronikus elmélete alapján magyarázható. Ehhez figyelembe kell vennünk az anyagon átmenő elektromágneses hullám kölcsönhatását, az elektronokban pedig az anyag atomján. Az elektronok mozgása egy atomban betartja a kvantummechanika törvényeit, és ennek a problémának a megfontolása jelentős nehézségeket okoz. Azonban, amint azt Lorentz is szemlélteti, számos optikai jelenség minőségi megértéséhez elegendő ahhoz, hogy az atom elektronjai közötti kvázi-rugalmas kötés létezésére támaszkodjunk. Az egyensúlyi helyzetből való eltávolítás során az ilyen elektronok ingadoznak, fokozatosan elveszítik a vibrációs energiát az elektromágneses hullámok sugárzásához. Ennek eredményeként az oszcilláció csillapodik, és a csillapítás figyelembe vehető a sebességgel arányos "súrlódási csillapító erő" bevezetésével.

piros narancssárga zöld kék kék ibolya
Amikor egy elektromágneses hullám áthalad az anyagon, az anyag atomjában lévő elektronra hatással van az elektromágneses mező oldalán lévő Lorentz-erő. Ez az erő:
ahol e - a töltés egy elektron, - elektromos mező, - az elektron sebessége az anyagban, - a mágneses mező, - a mágneses térerősség indukcióval összefüggő arány (esli = 1).
Számítás azt mutatja, hogy a kifejtett erő az elektronok által a mágneses mező 10 4-szer kevesebb, mint az erő a villamos tér, így a második kifejezés a Lorentz-erő lehet elhanyagolni, és úgy vélték, hogy csak hat az elektron erő által az elektromos mező. Mivel ez az erő a harmonikus törvényektől függően változik, ez a hajtóerő, és az elektron rezgései kényszerített oszcillációkat eredményeznek.
ahol 0 az elektron oszcilláció kezdeti fázisa, melyet a koordinátái határozzák meg. E0 az áramerősség amplitúdója, és a vektor oszcillációinak ciklikus frekvenciája a fényhullámban.
Az atom elektronra gyakorolt kényszerítő erőn túl, egyszerűsített feltételezéseink alapján a visszatérő QUASI-
ahol x az elektron egyensúlyi helyzetből való elmozdulása, k a merevségi együttható, és 0 az atomban lévő elektron-oszcillációk OWN ciklikus frekvenciája.
A számítások egyszerűsítése érdekében elhanyagoljuk a sugárzás csillapítását. Ezután ezeknek az erőknek a hatása alatt az atom elektronja oszcilláló mozgást hajt végre, a differenciál egyenlet, amelynek formája:
A differenciálegyenletek elméletéből ismert, hogy a (4) megoldás a következő alakú: x = xmaxsin (t + 0). ahol az amplitúdó
Vegyük szemügyre az elektronikus diszperziós elméletet. Az egyszerűség kedvéért feltételezzük, hogy az anyagmolekulák nempolárisak, azaz a molekulákat csak dipólusokká alakítják át külső elektromos mező hatása alatt. Továbbá, mivel a magok tömege az elektron tömegével összehasonlítva nagy, nem hagyjuk el a magok elmozdulását az egyensúlyi helyzetből a könnyű hullám hatására. Ebben a megközelítésben a molekula dipólus elektromos momentuma képviselhető a következő formában: pi = exi max. ahol xmax az i-th elektron maximális elmozdulása az egyensúlyi helyzetből az elektromágneses hullám hatása alatt. Mivel a molekulában lévő elektronok 0i természetes oszcillációs frekvenciákat tartalmaznak. majd a (5) kifejezést a molekula dipólus elektromos momentumának expressziójával helyettesítjük:
A molekulák számát egységnyi térfogattal jelöljük N betűvel. Az Np termék polarizációs vektort ad, amely a dielektrikumok elméletéből következően P = Np = 0E értékkel egyenlő. ahol 0 a vákuum elektromos állandója, a dielektromos érzékenység az anyag dielektromos permittivitásával összefüggésben:
Az átlátszó dielektrikumok törésmutatója, majd a
Mint látható a (8) a törésmutatója egy anyag az a frekvencia függvényében a beeső fény (ld. 2), és ez a függés egy rezonáns jellegű. Más szóval, a frekvencián jelentősen eltér minden sajátfrekvenciákkal 0i elektronok összeg (8) kicsi lesz képest egységet úgy, hogy n2 1. A törésmutató ebben az esetben növeli a frekvenciát a beeső fény ( 0) és a diszperzió NORMÁL DISPERSION.
Az 0i sajátfrekvenciák mindegyikénél a (8) függvény megszakadt: ha balról balra 0i közeledik, akkor + turns -ra változik. amikor jobbra fordul - in - (szaggatott vonal a 2. ábrán).
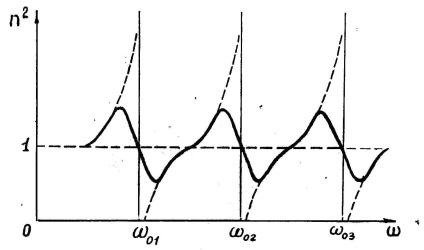
Ez a funkció (8) viselkedése annak a ténynek köszönhető, hogy elhanyagoltuk a "sugárzási súrlódást". Az oszcilláció elméletéből következik, hogy a súrlódás hiányában a kényszerített oszcillációk amplitúdója végtelenül rezonánsvá válik. A sugárzás súrlódásánál az n2 függése -re változik. a 2. ábrán látható egy szilárd görbe. A 0i régióban a törésmutató növekvő gyakorisággal csökken ( 0). Ezt a régiót az ANOMALO DISPERSION régiónak nevezzük, és megfelel a fény anyag általi felszívódásának.
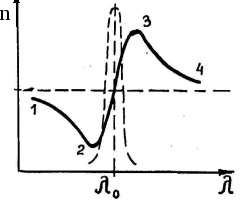
Átmenő n2-ről n-re és -ről -re. a 3. ábrán látható n = f () görbét kapjuk (csak az λ0i rezonancia hullámhosszak valamelyik régiójának görbéjét adjuk meg). Az 1 -2 és 3 - 4 görbék a normál diszperzió ( 0) tartományának és a 2 - 3 szakasznak felelnek meg az anomális diszperziónak (0).
Minden átlátszó színtelen anyag esetében az n = f () függvény egy karaktert tartalmaz a spektrum látható részében, a 3. ábrán a 3. - 4. görbe részben.
Amint a 3. ábrán látható, ahogy a fény hullámhossza áthalad az anyagon, a törésmutató csökken. Ebből következik, hogy a lilás sugarak a legnagyobb visszaverődésen mennek keresztül a trihedral prizmában, a diszperziós spektrumban az ibolya szín közelebb áll a prizma alapjához.