Mi a vándorlás a piziadas gráficas geometriájában?
Az egyik feltétel, amelyet több alkalommal kértem az osztályban az "Involution" -tól. Meghatározzuk az involúciókat.
Mi az Involution?
Az elsõ közelítésre törekszünk a Diccionario de la Lengua Española-ban
"A folyamat előrehaladásának vagy fejlődésének elmulasztása" [1]
A latin származás az "Involutio", az "Involutionis", a "csomagolás" kifejezést jelenti.
Látjuk, hogy a kifejezés az ellenkező műveletet jelenti, amelyet önmagán végzünk.
Mi a forradalom a matematikában?
Ha az x transzformációt az X-elem x elemére alkalmazzuk, megkapjuk a transzformált x '-t. Ezt f (X) = x '-ként fejezhetjük ki.
Az Involution olyan átalakulás, amely ismét alkalmazza az átalakítások elemét az előző transzformációkhoz, megkapja a kezdeti elemet
φα (φα (X)) = x
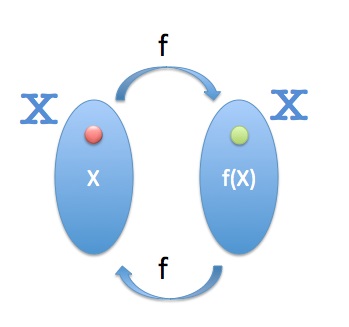
Mi a geometriai vívódás?
A geometriában a matematikai elemek grafikus ábrázolásával dolgozunk. Mindegyik pontra, a vonalra vagy a matematikai jelölésminták szintjére vonatkozóan megtaláljuk, ami azt jellemzi, ezért elvileg nem szabad különbséget tenni a fenti definíciók tekintetében.
Azonban az elemek, amelyeket akkor is használunk, még akkor is, ha absztraktak, bizonyos entitások (pl. Geometriai alakok pontjai) manipulálhatók, mivel ez lehet, érdemes beszélni az "involúciós átalakításokról", hogy közelebb kerüljenek a koncepcióhoz a grafikus műveletekben.
A véletlen fogalom rövid bemutatásának megvitatására olyan példákat lehet megvitatni, amelyek elmagyarázzák nekünk ezt az elképzelést.
Egyszerűen a vektoros átalakulás a szimmetria, az axiális és az energetikai növények. Ha a P pontokat P 'szimmetriákra használjuk, akkor azonnal látni fogjuk, hogy ismételten alkalmazzuk az átalakulást P-re, Q-t hívva, a mutált Q' megfelel a P eredeti elemének.
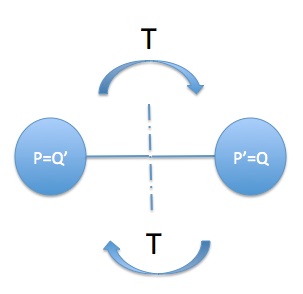
Ezt nem szabad fordított inverz átalakulásként értelmezni. Most ez az utolsó lehet olyan ember átalakulására, aki nem involutív.
Néhány geometriai transzformáció nem involutív, és általában bármely konkrét esetben alkalmazható. A forgatás nem véletlenszerű, de ha a forgásszög 180 °, ha igen, akkor.
Ezeknek a fogalmaknak a specifikus alkalmazása a projektív átalakításokban megtalálható a sorozatban és az első és másodrendű kötésekben az involúcióban.