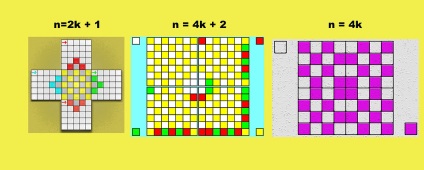
Mágikus tér
A teraszok módszere
Leírta Yu V. Chebrakov a "The Magic of Magic Mátrixok" című könyvében.
Egy adott furcsa n esetében húzzon egy négyzet alakú táblát az n méretből n-be. Ezt a táblázatot a terasz mind a négy oldalán (piramis) csatoljuk. Ennek eredményeként lépcsős szimmetrikus alakot kapunk.
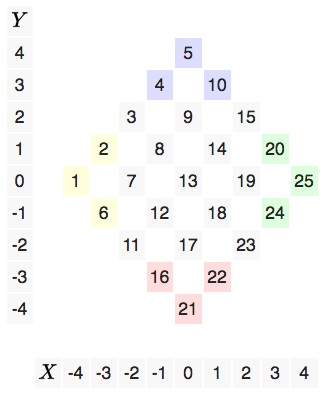
A lépcsősor bal oldali csúcsából kiindulva töltse át az átlós sorokat egymás után következő természetes számokkal 1-től N 2-be.
Ezután az N-edik sorrend klasszikus mátrixának megszerzéséhez a teraszokon lévő számokat azokon a helyeken kell elhelyezni, amelyek az N x N méretűek. Olyan lett volna, ha a teraszokkal együtt mozogtak, amíg a teraszok bázisai az asztal túloldalára nem kerültek.
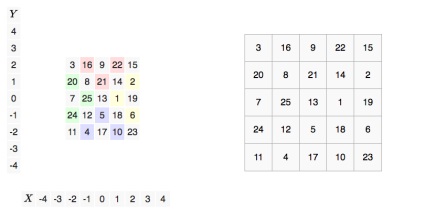
Emellett ez a módszer akkor is igaz, ha a mágikus tér nem az 1-től N-ig terjedő számokból áll. de K-től N-ig is, ahol 1 ≤ K 4. A legegyszerűbb konstrukció a mágikus (i, j) négyzetes, furcsa sorrendű. A számot a cellába kell helyezni a koordinátákkal
N + ((i + j + (n + 1) / 2) mod n) 1 + ((i-j + (n-1) / 2)
* Ennek a műveletnek a végrehajtása során negatív értékeket lehet elérni a mátrix jobb felső sarkában. Ebben az esetben hozzá kell adnunk az n 2-et és az eredményül kapott negatív számot. Meg kell azonban jegyezni, hogy a kapott négyzet félig varázslatos lesz.
Még könnyebb az építést a következő módon elvégezni. Az n x n mátrixot veszik. Belül egy lépcsős gyémánt épült. Ebben a bal oldali cellák felfelé az átlósak páratlan pár sorral vannak kitöltve. Meghatározzuk a C központi C értékét. Ezután a mágikus négyzet sarkában az értékek a következők lesznek: jobb felső cella C - 1; alsó bal C + 1 sejt; jobb alsó jobb cella C - n; a bal felső C + n.
Az üres cellák kitöltése lépésenkénti háromszögekben egyszerű szabályok betartásával történik:
1) a számsorok balról jobbra történő növelésével n + 1 lépéssel;
2) az oszlopokról fentről lefelé, a számok az n - 1 lépéssel nőnek.
Pandagonális négyzetek létrehozására szolgáló algoritmusokat, valamint ideális 9x9 mágikus négyzeteket is fejlesztenek. Ezek az eredmények lehetővé teszik számunkra, hogy az n = 9 (2k + 1) megbízások ideális mágikus négyzetét k = 0,1,2,3-ra állítsuk össze. . Vannak olyan általános módszerek is, amelyek lehetővé teszik az ideális, páros, mágneses négyzetek n> 3-át. Az n = 8k, k = 1,2,3 ... ideális mágikus négyzetek létrehozására szolgáló módszerek kifejlesztésre kerültek. A páratlan sorrendű pandiagonal és ideális négyzeteket csak akkor lehet összeállítani, ha azok nem szokványosak. Mindazonáltal szinte pandiagonal négyzetek találhatók. A tökéletes tökéletes mágikus négyzetek (hagyományos és nem hagyományos) különleges csoportja megtalálható.
Példák összetettebb négyzetekre
Módszeresen szigorúan kidolgozott mágikus négyzetek páratlan sorrendben és a kettős paritás sorrendjében. Az egyetlen paritás sorrendjének négyzetének formalizálása sokkal nehezebb, amint azt az alábbi rendszerek szemléltetik:
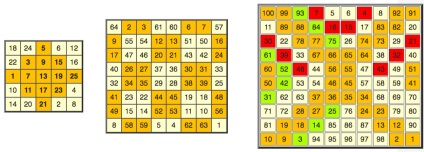
Több tucat más módszer létezik mágikus négyzetek létrehozására
Sakk megközelítés
Ismeretes, hogy a sakk, mint a mágikus négyzet, több tucat évszázaddal ezelőtt jelent meg Indiában. Ezért nem véletlen, hogy a varázslatos négyzetek építésének sakk megközelítése felmerült. Ez a gondolat első ízben Euler kifejezésre jutott. Megpróbált egy teljes mágikus térre jutni, folyamatosan a lovat keresztezve. Ez azonban nem sikerült, mivel a fő átlósban a számok összegei eltértek a mágikus konstanstól. Mindazonáltal, a sakk bontása lehetővé teszi, hogy létrehozz egy mágikus négyzetet. A számok rendszeresen töltődnek, és vonalban vannak a cellák színével.