A teljes áram törvénye
Legyen egy tetszőleges zárt vonal, amely áthatol egy vezetékkel egy árammal (1. ábra), vagyis egymáshoz illeszkednek két láncszemként. A vezeték körül egy mágneses mező jelenik meg.
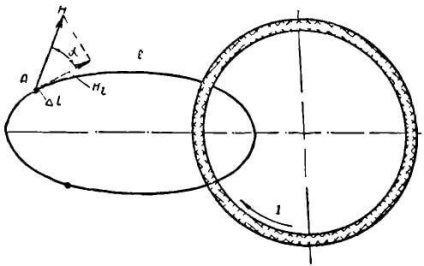
1. ábra. A teljes áram törvénye
Hozza létre az A ponton lévő áram által létrehozott H. feszültség vektorát. Ha a vonal több vezetéket fed le árammal, akkor minden egyes áramhoz feszültségvektorok épülnek fel a vonal adott pontján. A geometriailag különálló erősségű vektorok hozzáadásával megtaláltuk a kapott mágneses térerősség vektorát.
A kapott H feszültség vektora általában egy hosszúságú elemzel van kialakítva # 916; l szög # 945; Ezért a keletkező H feszültség Hl hosszanti vagy tangenciális komponense:
Ha az osztott vonal zárva n elemek hosszának és összehajtogatott termék hossza valamennyi elemét a tangenciális komponensei eredő erő a ezeket az elemeket, megkapjuk a következő összeget:
Ez az összeg a következőképpen jeleníthető meg:
ahol a jel a k = 1-től k = n-ig terjedő összeget jelöli.
Az elméleti elektromos bebizonyította, hogy az összeg egyenlő az algebrai összege áramok folytató összegzés, hasonló áramkör milyen egy reteszelő két szomszédos láncszem.
Ezért írhatunk:
Ezt a megfogalmazást a teljes áram törvényének nevezik. Abban az esetben, amikor a kontúr ismételten átmegy ugyanannak a tekercsnek, például például több tekercses tekercs jelenlétében. a teljes áram:
Ha a zárt tömörítési hurok egybeesik a mágneses vonallal, akkor a kontúr bármely pontján a feszültségvektor a hosszúságú elem érintője mentén irányul # 916;
és a teljes áram törvénye a következőképpen alakul:
Ha a kontúr minden pontján az erő értéke megegyezik, és az összeg # 916; l a kontúr mentén egyenlő l. akkor a teljes áram törvényének képletét a következőképpen írjuk:
A teljes áram törvénye a mágneskörök számításakor a legfontosabb törvény, és bizonyos esetekben lehetővé teszi a térerősség könnyű meghatározását.
Például, ha a teljes áram törvényét alkalmazzuk annak érdekében, hogy meghatározzuk az egyenes vonalvezetővel és egy áramerősséggel távozó távolságot, akkor:
2. ábra. Egy gyűrű köré tekercselt tekercs térerősségének meghatározása
A tekercsben a gyűrű köré tekeredő térerősség meghatározásához (2. ábra) ismét a teljes áram törvényét használjuk. A kontúr itt egy r sugarú kör. A kontúr permeálja a w irányokat egy irányba:
A gyűrű középvonalának hossza l = 2 × π × r. kapunk:
Így, a feszültség tekercs mezőt arányos a termék számának amper fordul számát vagy ampermenetek. I × w nevezzük mágnesezési erő és betűvel jelölt F. Mivel w - száma az absztrakt, a mágnesezési erőt mérjük amper.
A tekercsben lévő mágneses indukció:
Ha a gyűrű keresztmetszete a teljes hosszúság mentén ugyanolyan és egyenlő S-vel, akkor a B. mágneses indukciót ismerve meg lehet határozni a mágneses fluxust:
Ugyanez a képlet más formában is megjeleníthető:
Szerkezete szerint ez a képlet hasonlít az Ohm képletére. Fent említettük, hogy az I × w terméket Ikalmazza a mágnesező erő. A nevezőn belüli kifejezést mágneses ellenállásnak nevezik, és az Rm betű jelöli:
Ebből a képletből látható, hogy a mágneses ellenállás arányos az út hosszával és fordítottan arányos az anyag keresztmetszetével, amelyen keresztül a mágneses fluxus áthalad.
Így a mágneses fluxus arányos az F mágnesező erővel és fordítottan arányos az Rm mágneses ellenállással:
3. ábra A vákuum teljes áramának törvénye
Forrás: Kuznetsov M.I. "Az elektrotechnika alapjai" - 9. kiadás, felülvizsgált - Moszkva: Felsőoktatás, 1964 - 560-as évek.