A háromfázisú áramkör aszimmetrikus módja
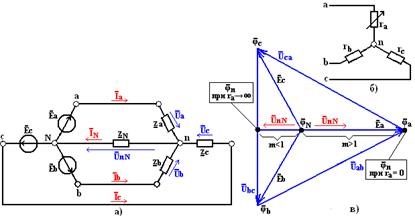
Az egyik leggyakoribb eseteit aszimmetrikus üzemmódban háromfázisú áramkört csatlakoztatásával egy csillag aszimmetrikus vevő fázisok nélkül nullavezető, vagy semleges huzal impedanciájú amelyet figyelembe kell venni a számítás (4a.).
A 4a. Ábrán látható áramkörnek két semleges pontja van: egy N szimmetrikus generátor és egy aszimmetrikus vevő - az áramkör két csomópontja. A működési mód kiszámításához az interstitiális stressz képletét használjuk. A számított háromfázisú rendszerben a vevő és a generátor semleges pontjainak feszültsége közötti komplex értéket a semleges torzítási feszültségnek nevezzük. Ez a feszültség
Figyelembe véve
hol van a fázis együttható, -
átírjuk (11) a formában
A fogadó feszültségét Kirchhoff második törvénye határozza meg:
Az Ohm törvénye szerint a fázisáramok és a semleges huzalban lévő áram egyenlő
Az aszimmetrikus vevő fázisai közötti feszültségek eloszlását, amelynek fázisai csillaggal vannak összekapcsolva, a lehetséges diagramban (4.
A potenciáldiagram felépítésében a nulla potenciál a generátor semleges N pontján van kiválasztva, amely referenciapontként szolgál. A referencia eredetétől a generátor fázisának három vektora van kialakítva. . . A vektorok végei meghatározzák a potenciál komplex értékeit. . lineáris vezetékek a. és következésképpen a lineáris igénybevételeket. . . Szimmetrikus vevőegységgel nincs semleges eltolás, vagyis a vevő semleges pontja. Ezért az ábrán a vevő semleges pontjának potenciálja egybeesik a generátor semleges pontjával. Aszimmetrikus vevővel a semleges eltolás nem nulla. Ezért a vevőegység semleges pontjának potenciálja eltolódik a generátor semleges pontjának potenciáljához viszonyítva. azaz A lineáris igénybevételek háromszögének közepétől.
Tekintsük a vevőegység legegyszerűbb esetét, ahol az aktív fázisrezisztensek ra és rb = rc = r semleges vezeték hiányában (4. A b és c fázisok vezetőképessége megegyezik: gb = gc = g = 1 / r, és az a fázis a = 1 / a vezetőképessége 0 és ∞ között változik. Feltéve, hogy ga / g = m, akkor a semleges elmozdulást határozzuk meg:
Ha a vezetőképesség ga változó nullától a végtelenig változik, az EMF tényező valós érték marad. Következésképpen a semleges bias feszültsége egy fázisban egyezik meg az EMF-rel m> 1, és m <1 их фазы отличаются на π (рис. 4,в). В частности, при размыкании фазы а. т.е. ga = 0 или ra → ∞ и m = 0, смещение нейтрали
A vevő feszültségének feszültsége
A ga → ∞ vagy ra = 0, azaz. amikor az a és n pontok rövidre záródnak. . .
A vevőegység semleges pontjának potenciálja messze túlmutathat a lineáris feszültségek háromszögén, ha a csillagfüggetlen vevőkészülékeknek a semleges huzal nélküli csillagok összekapcsolása eltérő jellegű.
A vevők összekötése háromszögben
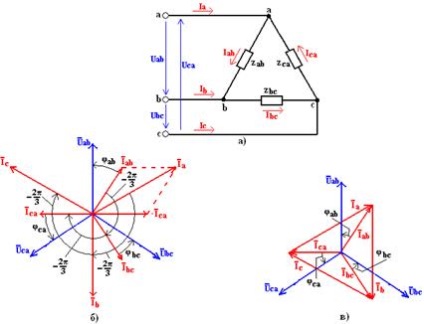
Amint az az 1. ábrán látható. 1, a, a vevő minden fázisa, ha háromszög csatlakozik, két lineáris vezetékhez van csatlakoztatva. Ezért, függetlenül a vevő ellenállásának értékétől és jellegétől, minden egyes fázisfeszültség megegyezik a megfelelő lineáris feszültséggel:
Ha nem veszi figyelembe a hálózati vezetékek ellenállását, akkor a vevő feszültsége egyenlő lehet a forrás vonali feszültségével.
Az első Kirchhoff-törvényt az a, b, c csomópontokra alkalmazva meghatározzuk a lineáris és a fázisáramok közötti kapcsolatokat:
A kapott kapcsolatok és a fázisáramú vektorok alkalmazásával nem nehéz megépíteni a lineáris áramok vektorát.
Minden fázis tekintetében az egyfázisú áramkörökre kapott összes képlet érvényes. Például,
Nyilvánvalóan szimmetrikus terhelés
A fázis és a lineáris feszültségek vektordiagramja, valamint a szimmetrikus aktívinduktív terhelés fázisáramainak ábrázolása a 3. ábrán látható. 1, b. Ugyanazon a helyen, a (2) kifejezéseknek megfelelően lineáris áram vektorok vannak kialakítva. A kapott kifejezésekből és a vektordiagramból következik, hogy szimmetrikus terhelés mellett léteznek szimmetrikus fázis- és lineáris áramlási rendszerek.
A lineáris áramok vektorai gyakran ábrázolják a megfelelő fázisáramok összekötő vektorait, amint azt az 1. ábra mutatja. 1, c.
A vektor diagram alapján
Egy szimmetrikus terhelésű háromfázisú vevő teljesítményének meghatározásához a csillagkapcsolathoz kapott képleteket használhatjuk.
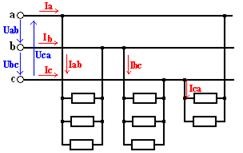
A csillagkapcsolathoz hasonlóan, háromszög csatlakozás esetén az egyfázisú vevőkészülékek három csoportra oszthatók, nagyjából egyenlőek a csoport teljesítményével. Mindegyik csoport két vezetékhez van csatlakoztatva, amelyek között feszültség van a hálózat két másik feszültségétől (2. ábra). Minden egyes csoporton belül a vevők párhuzamosan vannak csatlakoztatva.
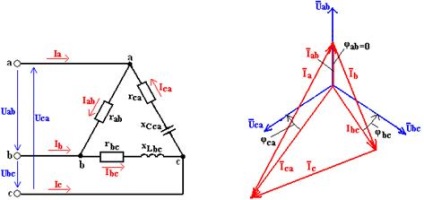
A fázisfeszültségek és áramok közötti fázisáramok, fázisszögek, valamint a fázisfeszültségek a (3) képletekből határozhatók meg. aszimmetrikus terhelések esetén a fázisáramok, a fáziseltolódási szögek és a fázisteljesítmény általában eltér.
A vektor diagramja az esetben, ha van egy fázis ab ohmos terhelés fázisban bc - aktív-induktív és fázisban ca - aktív-kapacitív (. Ábra a 3a) ábrán mutatjuk be. 3, b. A lineáris áramvektorok konstrukcióját a (2) szerint végezzük.
Az összes fázis hatáskörének meghatározásához képleteket kell alkalmazni
Ha a fázisáramok mellett lineáris áramok is szükségesek, akkor a problémát összetett formában kell megoldani. Ugyanebből a célból vektordiagramot használhatunk.
Amikor a problémát komplex formában megoldjuk, először is bonyolult formában kell kifejezni a fázisfeszültségeket, valamint a teljes fázisú ellenállásokat. Ezt követően könnyű meghatározni a fázisáramokat az Ohm törvénye szerint.
A lineáris áramokat a fázisáramok határozzák meg (2).
Integrált módszer is használható a fázishatások meghatározására. Például a phazeab hatásköre egyenlő