Kubos egyenletek
A legelterjedtebb hírnévnek köszönhetően a köbös egyenletek megoldásának keresése.
A legelterjedtebb hírnévnek köszönhetően a köbös egyenletek megoldásának keresése. A megvalósítás algoritmusa a következő.
Először az egyenlet gyökereit választjuk ki a tulajdonsággal, hogy a köbös egyenlet mindig legalább egy valós gyökeret tartalmaz. és a teljes együtthatókkal rendelkező köbös egyenlet integrális gyökere a szabad idő d osztója.
Az egyenletek együtthatói. Rendszerint úgy választják őket, hogy a szükséges gyökér egy kicsi egész szám. mint például: 0, ± 1, ± 2, ± 3.
Ennek megfelelően meg kell találni a gyökeret ezek között a számok között, és az egyenletbe történő helyettesítéssel ellenőrizni.
Vessük ezt a gyökeret, mint x 1.
A következő lépésben a binomiális x - x 1 bináris x + x 2 + cx + d polinomot osztjuk el.
Alkalmazzuk a tétel Bezout (lineáris többtagú részlege binomiális), miáltal lehetséges osztás maradék nélkül, és a számítások eredményeként megkapjuk a másodfokú polinom. amely nulla. A kapott kvadratikus egyenlet megoldása. megtaláljuk (vagy nem!) a másik két gyökeret.
Elemezzük az egyenlet megoldásának folyamatát: x 3 - 3x 2 - 13x + 15 = 0.
Megtaláljuk az első gyökeret, amely a 0, ± 1, ± 2, ± 3 számjegyeket helyettesíti az egyenletbe, és megkapjuk, hogy az 1 egy gyökér. Ezután ezt az egyenlet bal oldalát a binomiális x-1 segítségével osztjuk el és megkapjuk:
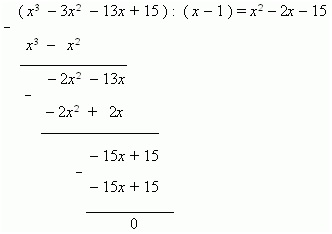
Ezután számolja ki a négyzetes egyenlet gyökereit. x 2 - 2x - 15 = 0.