Egyszerűsített set - enciklopédia - enciklopédia és szótárak
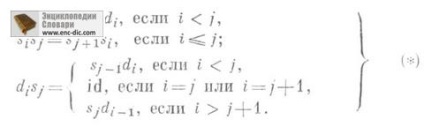
Meghívják a K n rost pontját. a C. K. n-dimenziós szimplexei. a dj = dj-1 di. én
Egy egyszerű leképezés f: K '- C'. a mûködõk morfizálása, vagyis a kapcsolatoknak megfelelõ leképezések sorozata,
Minden topológiára. Az X helyet az SM S (X), n. egy X tér szimultán elosztója, amelynek szimplexei az X tér (lásd Singular homology) szinguláris egyszerűsége, azaz folyamatos leképezések. ahol D n az n-dimenziós geometriai standard szimplex
Ezt a SM arcát és a degenerációját a képletek határozzák meg
Az SM K (p) valójában egy egyszerű csoport.
Minden Abel-csoport p és bármely egész m határozzuk pp. (Sőt, egy simplicial Abel-csoport) E (p, n), szimplexek dimenzió Qc-cerned vannak újra dimenziós cochains Q-dimenziós geometriai standard szimplex D Q együtthatók π csoport (tehát E (p, n) q = C n (Dq; p)). A Dq szimplex csúcspontjait szimbólumokkal jelöljük, egyszerűsített leképezéseket és képleteket definiálunk
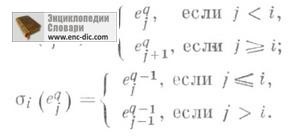
A cochain csoportok indukált homomorfizmusa
definíció szerint az E (p, n) terület határa és degeneráltsága. A ciklusok egyszerűsítései az E (p, n) egy egyszerű részhalmazát képezik, Eilenberg-MacLane polinomot, és K (p, n) jelöli. A C * (Dq; p) csoportok határátengelye egy kanonikus egyszerűsített leképezést határoz meg (d, d, d, d). Mivel egy egydimenziós ciklus koncepciója is van értelemben egy nem abeliai csoport számára (lásd a nem abeliai kohomológiát), az SM K (p, 1) meghatározása anélkül feltételezhető, hogy a p csoport abelianus. Ez a CMM + (K) izomorf, és hívják. (co) homológ csoportjai. Az SM K (p) (co) homológia csoportjai a p csoport (co) homológ csoportjai.
Simplex S. m. Knaz. degenerálódik, ha ilyen szimplex és degenerációs operátor létezik olyan, hogy x = si y. Lemma Eilenberg- - Zilber azt állítja, hogy minden simplex S. m Kedinstvennym képviselt formájában x = K (k) y, ahol egy bizonyos S- epimorphism-nek, és a -. Nem degenerált simplex. A legkisebb részhalmazát S. simplicial m. K, amely tartalmazza az összes annak degenerált szimplexek mérete kisebb vagy egyenlő, mint N, jele N vagy K Sk n K és az úgynevezett. n-dimenziós csontváz C. m. K.
Geometriai standard szimplexek
egy kozimpliciai topológiát alkotnak. a tárcák és az együttes előfordulások operátorai tekintetében. képletekkel meghatározott
Egy diszjunktúrában, ahol minden K n-t diszkrét halmaznak tekintünk, képleteket
meghatározzák ekvivalens aránya, a hányadosa egy k-rum sejt bomlás (celluláris térben), sejt-a-cerned vannak bijektív levelezés nem degenerált m cimpleksami S. K. Ez a cella bomlás jelöljük. | A | | vagy RK és hívott. geometriai megvalósítás Milnor SM K értelmében. Minden egyes egyszerű térképet a képlet segítségével indukál
folyamatos leképezés, és a megfeleltetések reprezentálják az R funktort. Ez a funktor a bal oldali konjugátumtól függ. A megfelelő funkciók izomorfizmusa
A konjugációs morfizmus minden topológiás. A tér gyenge homotopia. ekvivalencia (ez különösen azt bizonyítja, hogy egy tetszőleges topológiai tér gyengén homotopi egyenértékű a sejtes bomlással).
Az építmény geometriai. végrehajtás A | | általánosítható topológiai topológiára. space K. Lehetséges. szintén definiálják a Giver-Hoo || K || értelmében vett geometriai megvalósítást, amely figyelembe veszi csak az arc operátorokat di (ebben a megvalósításban vannak cellák a K összes szimplexje számára, és nemcsak a nem degeneráltak). Ha minden degeneráló operátor egy zárt kofibráció (egy feltétel, amely automatikusan teljesül egy metrikus térben), akkor a természetes térkép homotopiás. egyenértékűségét.
Különösen, minden CM esetében a terméke egy egyszerű D 1 szegmensre van definiálva. Az előrejelzések meghatározzák a bijektív térképezést
amely homeomorfizmus, amikor az RK X RL termék egy sejtbontás (pl. ha mindkét CM megszámolható, vagy ha az egyik RK vagy RL sejtosztály lokálisan véges). Ebből különösen az következik, hogy geometriai. Valamely megszámlálható egyszerű monoid (egy csoport, Abel-csoport) megvalósítása topológiai. monoid (csoport, Abel csoport).
Egyszerű térképeket hívnak. homotópikusak, ha létezik olyan egyszerű homogenizálás (homotopia) L, hogy
minden szimplexre és minden s (n hosszúságú) összetételre a degenerálódási operátorok számára. Ez a definíció (amely a folyamatos leképezések homotópiájának szokásos definícióját szimulálja) egyenértékű (SM esetében) az egyszerű objektumok egyszerűsített leképezéseinek homotópiájának általános meghatározásával.
A szabványos font (Simple standardx) egyszerűsített leképezése a Banach terekben. Mindegyik fontot egyedileg határozzák meg az n-dimenziós szimplexek x 0 x1 (n + 1) tagú szekvenciájával. xk-1. xk + 1. xn + 1, amelyre di xj = dj-1 xi bármelyik számára. Azt mondják, hogy egy font töltött, ha kiterjed az egész SM D n + 1-re. azaz létezik egy (n + 1) -dimenziós szimplex x, így di x = xi mindegyikhez. S. m. Knaz. teljes (vagy kielégíti a Kahn-feltételt), ha mindegyik font töltött.
amely minden SM-hez egy teljes CMS-t korrelál, geometriai. amelynek megvalósítása homotópikusan egyenértékű a geometriai jellemzőkkel. a S. m. Ki-rozsának megvalósítása ezért teljes mértékben felváltja a homotopiás kérdések CM-jét.
Két n-dimenziós szimplex xi x 'C. Knas. összehasonlítható, ha. Hasonló szimplexeket neveznek. homotópikus, ha van (n + 1) -dimenziós szimplex y, hogy dn y = x, dn + 1 y = x 'és di y = sn-1 di x = sn-1 di x'. . A teljes C. m. Ez egy ekvivalencia reláció, a szimplexek IFF homotóp, amikor azok jellemző simplicial kijelzőn homotóp.
S. m. Knaz. Egy hegyes, ha jelölve egy bizonyos nulla dimenziós szimplex-nek q (ugyanaz a jel q minden degeneráció e simplex és generált simplicial részüket, to-Roe szokás nevezni. markáns pont K). Egy teljes lyukú SM számára a homotóp "-dimenziós szimplexek pn (K) -osztályai, amelyek hasonlóak a simplex q-hez, egy csoporthoz tartoznak. Ezt a csoportot hívják. n-m ernoy homotóp csoport kilyukadt teljes C. m K, ez a terminológia a tény indokolja, hogy a PN (K) .PP (| K |), és különösen pn (K (p, n)) = P és PI (K. (p, n)) = 0 a. CM, amelyre minden pi (K) .0 mindenki számára nevezik. n-csatlakoztatva; Ezenkívül egy 0-kapcsolt SM-t nevezünk. csatlakoztatott, és az 1-csatlakozó SM egyszerűen csatlakoztatva van. Egy olyan csoport hozzáadása által kiváltott művelet társítja szimplexek chi y (összehasonlítható q) szimplex DN Z, ahol Z - Szimplex n dimenziós + 1, töltse cornetus xi = 0, és X n-1 = x, x n + 1 = y. Ha C. m. Kyavlyaetsya simplicial monoid identitás q, majd az adagolást indukált szintén ebben monoid szorzás (a két termék szimplexek összehasonlítható q, összehasonlítható q).
Mivel a q-hez hasonló bármely szimplex γ egy ciklus (a C (K) lánc komplex, amelyet az SM határoz meg), akkor egy természetes homomorfizmus
Gurevich, η = 1, az indukáló izomorfizmus
(Poincaré tétele), és n> 1 esetében ez egy izomorfizmus, amikor az SM K (n-1) kapcsolódik (Hurewicz tétele). A teljes SM esetében a Whitehead-tétel mindkét változatában érvényes, vagyis a teljes SM egyszeres leképezése, ha és csak akkor, ha homotopi. ekvivalencia, ha homotópiás izomorfizmust indukál. csoportok, és egyszerűen összekapcsolt félcsoportok esetében ez a feltétel egyenértékű azzal a ténnyel, hogy a homológ csoportok indukált homomorfizmusai izomorfizmusok.
Abban az esetben, ha R jelentése egyszerű csoport, a pn (K) csoport izomorf a lánc (nem feltétlen abelian) komplex homológ csoportjához, amelyhez