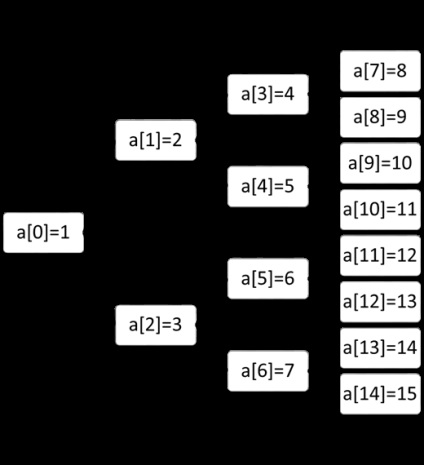
Bináris fa reprezentálása tömbként
Hivatkozásokat. 15
A tömbök és a kapcsolódó listák meghatározzák az egymás után elérni kívánt objektumok gyűjteményét. Az ilyen adatstruktúrákat lineáris listáknak nevezzük, mivel egyedülálló első és utolsó elemeik vannak, és minden belső elemnek csak egy utódja van. Egy lineáris lista egy absztrakció, amely lehetővé teszi a különböző módon - tömbök, kötegek, sorok és összekapcsolt listák - által képviselt adatok manipulálását.
Számos alkalmazásban egy nem-lineáris objektumot érzékelnek, ahol az elemeknek több örököse is lehet. Például a családfán a szülőnek több gyermeke is lehet (gyermek). Az 1. ábrán. Az 1. ábra a család három generációját mutatja. Ezt a rendelést hierarchikusnak hívják.
Ebben a cikkben egy nem-lineáris struktúrát fogunk megnevezni, amely csomópontokból és ágakból álló fa, és amelynek iránya a gyökértől a külső levelekig terjed. Ezek a struktúrák hasonlóak a 6. ábrán látható kommunikációs hálózathoz. 2, speciális algoritmusokat igényelnek és speciális alkalmazásokban használatosak.
A fa szerkezetét egy csomópont (csomópont) alkotja, amely egyetlen kezdő csomópontból származik, a gyökérnek nevezik. Az 1. ábrán. 3 az A csomópont. A genealógiai fa szempontjából a csomópont szülőnek tekinthető 0, 1 vagy több csomópontnak, gyermekeknek nevezhető. Például a B csomópont az E és F fiai szülője. A H csomópont szülője a D. csomópont. A fa a család több generációját képviselheti. A csomók fiait és fiaik fiait leszármazottaiknak nevezik, és a szülők és a nagyszülők a csomó ősei. Például az E, F, I és J csomópontok a B csomópont leszármazottai. Minden nem gyökércsomópontnak csak egy szülője van, és minden szülőnek 0 vagy több fia van. A gyermeket nem tartalmazó csomópontot (E, G, H, I, J) levélnek nevezik.
Minden fa csomópont a szubtróna gyökere, amelyet ennek a csomópontnak és a csomópont összes gyermeke határoz meg. Az F csomópont az F, I és J csomópontokat tartalmazó részalap gyökere. A G csomópont a szubtróna gyökere leszármazottak nélkül. Ez a definíció lehetővé teszi számunkra, hogy azt mondjuk, hogy az A csomópont a szubtree gyökere, amely maga is fa.
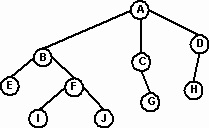
A szülőcsomópontról a gyermekcsomópontra és más gyermekekre való átmenet az út mentén történik. Például a 3. ábrán. 4 Egy út a gyökértől a csomópont F nyúlik ki, hogy a B és a B és F Az a tény, hogy minden nem-gyökér csomópont egyetlen szülő, biztosítja, hogy van egy egyedülálló út a minden csomópont annak a gyermekek. A gyökértől a csomópontig terjedő út hossza a csomópont szintje. A gyökérszint 0. A gyökér minden fia az 1. szint csomópontja, a következő generáció a második szint csomópontjai, és így tovább. Például a 3. ábrán. 4 csomópont F a 2. szint csomópontja, amelynek hossza 2.
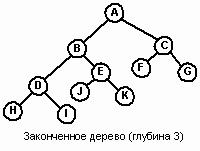
A fa mélysége a legmagasabb. A mélység fogalmát az útvonal szempontjából is leírhatjuk. A fa mélysége a leghosszabb út hossza a gyökértől a csomópontig.
A 4. ábrán a fa mélysége 3.
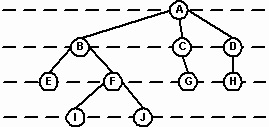
4. ábra. Csomópont szintje és elérési útvonala
Bár az általános fák eléggé fontosak, a fák korlátozott osztályára összpontosítunk, ahol minden szülőnek nincs több, mint két fia (5. ábra). Az ilyen bináris fák (bináris fák) egységes struktúrával rendelkeznek, amely lehetővé teszi a különböző átviteli algoritmusokat és az elemekhez való hatékony hozzáférést. A bináris fák tanulmányozása lehetővé teszi a fákkal kapcsolatos leggyakoribb feladatok megoldását, mivel egy általános fajtát egy hasonló bináris fa képviselhet.
A bináris fa minden csomópontja 0, 1 vagy 2 fia lehet. A bal oldalon lévő csomóponttal kapcsolatban a baloldali gyermek kifejezést fogjuk használni, és a jobb oldali csomóponthoz viszonyítva a megfelelő gyermek. A "bal" és "jobb" nevek a fa grafikus ábrázolására utalnak. A bináris fa rekurzív struktúra. Minden egyes csomópont a saját alfa gyökere. Ő fiai, akik maguk a fák gyökerei, azaz bal és jobb oldali részfalak. Így a fák feldolgozásának folyamata rekurzív. Itt van egy bináris fa rekurzív definíciója:
A bináris fa a B csomópontok halmaza
a) B egy fa, ha a csomópontok halmaza üres (egy üres fa is egy fa);
b) A B három diszjunkt szubpontra oszlik:
· A bal oldali R szubsztrát
· A jobb oldali R
Minden n szinten egy bináris fa tartalmazhat 1-2 csomópontot. A csomópontok száma szintenként a fa sűrűségének jelzője. Intuitív módon a sűrűség egy fa méretének (a csomópontok száma) mérete a fa mélységéhez viszonyítva. Az 1. ábrán. Az A fa 8 csomópontot tartalmaz a 3. mélységben, míg a B fa 5 csomópontot tartalmaz a 4. mélységben. Ez utóbbi esetben egy egyedi alak, mely egy degenerált fa, amelynek egyetlen lapja (E) van, és mindegyik nemleveles csomópont csak egy fiú. A degenerált fa egyenértékű egy összekapcsolt listával.
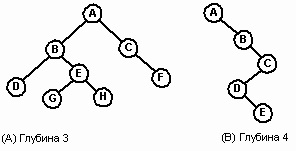
5. ábra. Bináris fák
A nagy sűrűségű fák nagyon fontosak, mivel adatszerkezetek, mivel arányosan több elemet tartalmaznak a gyökér közelében, azaz rövidebb útvonalakkal a gyökérből. A sűrű fák lehetővé teszik a nagy adatkészletek tárolását és az elemek hatékony elérését. Gyorskeresés - a legfontosabb dolog, ami a fák használatát teszi lehetővé az adattároláshoz.
A degenerált fák a sűrűség végső mértéke. A másik extrém az N mélységű bináris fa, ahol minden egyes 0. N-1 szintnek van egy teljes csomópontja, és az N szint minden levele balra van. Az N szinten 2N csomópontot tartalmazó teljes bináris fa kész. Az 1. ábrán. A 6. ábra a teljes és teljes bináris fákat mutatja.
6. ábra. A bináris fák osztályozása
A bináris fákat számos funkció jellemzi. Bemutatjuk a csomó fokának és a fa fajtájának fogalmát. A fa csomópontjának mértéke az ívek számát jelenti, amelyek abból származnak. A fa mértéke megegyezik a fa belépő csomópont maximális fokával. Az oklevel definíciója alapján nyilvánvaló, hogy egy bináris fa csomópontjának mértéke nem haladja meg a kettőt. Ebben az esetben a fa levelek olyan csúcsok, amelyek nulla fokozattal rendelkeznek.

7. ábra. Bináris fa
A bináris fák szerkezeti osztályozásának másik fontos jellemzője egy bináris fa szigorúsága. A szigorúan bináris fa csak olyan csomópontokból áll, amelyek két fokkal vagy nulla fokozattal rendelkeznek. Az értelmetlen bináris fa olyan csomópontokat tartalmaz, amelyeknek megegyezik egy.

8. ábra. Teljes és hiányos bináris fák

9. ábra. Szigorúan és nem szigorúan bináris fák
A bináris fák könnyen ábrázolhatók listák vagy tömbök formájában. A bináris fák listázott ábrázolása a fa csomópontjainak megfelelő elemeken alapul. Minden elemnek van egy adatmezője és két mutató meze. Egy mutató segítségével az elemet a jobb gyermekhez lehet kapcsolni, a másik pedig balra. A levelek üres mutatói vannak a leszármazottaknak. Ezzel a fa ábrázolásával mindig mutasson egy mutatót a csomópontnak, amely a fa gyökere.
Megfigyelhető, hogy a reprezentációnak ez a formája hasonló az egyszerű lineáris listákhoz. És ez a hasonlóság nem véletlen. Valójában a bináris fa ábrázolásának módja egyfajta multisesszió, amelyet egy sor lineáris listák kombinációja alkot. Minden egyes lineáris lista kombinálja azokat a csomópontokat, amelyek az ösvényt a fa gyökerétől az egyik levelig belépték.

10. ábra. A bináris fa reprezentációja listaszerkezet formájában
Táblázatos formában a teljes bináris fa legegyszerűbben ábrázolható, mivel minden szinten szigorúan meghatározott számú csúcsot tartalmaz. A csúcsok egymás után balról jobbra számozhatók a szintek szerint, és ezeket a számokat indexként egydimenziós tömbben használhatjuk.

11. ábra. Bináris fa reprezentálása tömbként
Ha a fa szintjeinek száma nem változik jelentősen a feldolgozás során, akkor egy teljes bináris fa reprezentálása ezáltal sokkal gazdaságosabb lesz, mint bármelyik listák szerkezete.
A bináris fa reprezentált módjának fő hátránya, hogy az adatszerkezet statikus. A tömb méretét a bináris fák maximális lehetséges szintje alapján határozzák meg. És annál kevésbé teljes a fa, annál kevésbé racionálisan használják a memóriát.
Például arra, hogy egy bináris fát tömbként használunk, olyan tömböt használtunk - a [i], amely 15 elemből áll (1-től 15-ig). Ennek eredményeképpen a fának úgy kell kinéznie: