A vízmozgáshoz szükséges feladatok
Ez az anyag a "Mozgalom" témakör feladata.
A cél: segíteni a hallgatókat, hogy jobban elsajátítsák a problémamegoldás technológiáját ebben a témában.
A vízen való mozgás feladatai.
Nagyon gyakran egy személynek kell mozognia a vízen: a folyó, a tó és a tenger.
Először megcsinálta magát, majd a tutajok, csónakok, vitorláshajók jelentek meg. A technológiai gõzhajók, motoros hajók fejlesztésével a nukleáris hajók az ember segítségére jöttek. És mindig érdekelte az utazás hossza és a túlélés ideje.
Képzeld el, hogy a tavasz az utcán van. A nap elolvasta a havat. Pocsolyák voltak és patakokat futottak. Két papírozott hajót készítünk, és egyiket a pocsolyába tesszük, a második pedig a patakba. Mi fog történni mindegyik hajóval?
A pocsolyában a hajó állni fog, és a patak úszójában, ahogy a víz "lebeg" egy alacsonyabb helyre, és magával viszi. Ugyanez fog történni egy tutajjal vagy hajóval.
A tóban állnak, és a folyó vitorláján.
Tekintsük az első lehetőséget: egy tó és egy tó. A víz nem mozog benne, és állandó víznek nevezik.
Egy csónak csak egy pocsolyában fog lebegni, ha megnyomjuk, vagy ha a szél fúj. És a hajó evezőkön keresztül mozogni kezd a tóban, vagy motorral van felszerelve, vagyis annak sebessége miatt. Ez a mozgás álló vízben mozgalomnak nevezik.
Különbözik-e az út vezetésén? A válasz nem. És ez azt jelenti, hogy tudjuk, hogyan kell cselekedni ebben az esetben.
Feladat 1. A hajó sebessége a tó mentén 16 km / h.
Miféle út a hajó 3 óra múlva halad át?
Nem szabad megfeledkezni arról, hogy a hajó sebességét álló vízben saját sebességének nevezik.
Feladat 2. A tó 60 kilométeres körzetében úszott egy 4 órás motorcsónak.
Keresse meg a saját motorját.
3. feladat: Mennyi ideig tart egy hajónak, amelynek saját sebessége van?
28 km / h a tó partján 84 km?
Tehát annak érdekében, hogy megkeressük a haladási útvonal hosszát, meg kell szorozni a sebességet.
A sebesség megtalálásához szükség van arra, hogy az út hosszát időben felosztjuk.
Az idő megtalálásához az útvonal hosszát a sebességgel kell osztani.
Mi a különbség a tó forgalma és a folyó mentén történő mozgás között?
Emlékezzünk egy patinás hajóra a patakba. Hajózott, mert a víz mozog benne.
Ez a mozgás az aktuális áramlásnak nevezik. És az ellenkező irányba - mozgás a jelenlegi ellen.
Tehát a víz a folyóban mozog, ezért saját sebessége van. És ezt nevezik a folyó áramának gyorsaságának. (Hogyan mérjük meg?)
4. probléma: A folyó sebessége 2 km / h. Hány kilométert visz a folyó
bármely tárgy (egy chip, tutaj, csónak) 1 órán át, 4 órán keresztül?
Válasz: 2 km / h, 8 km / h.
Mindannyian a folyón hajóztak, és emlékeznek arra, hogy sokkal könnyebb úszni az árammal, mint az árammal szemben. Miért? Mert az egyik irányba a folyó "segít" úszni, és a másik irányba "akadályozza".
Azok, akik nem tudják úszni, elképzelhetik a helyzetet, amikor erős szél fúj. Tekintsünk két esetet:
1) a szél fúj a hátulról,
2) a szél fúj az arcba.
És mindkét esetben nehéz megy. A szél a hátán arra kényszerít bennünket, hogy futassunk, ami azt jelenti, hogy mozgásunk gyorsasága növekszik. Az arcon levő szél kopog, lefék. A sebesség csökken.
Tartsuk mozgásban a folyó mentén. Már beszéltünk egy papírcsónakról egy tavaszi patakról. A víz magával viszi. És a hajó, amely a vízbe indult, az áram sebességével hajózik. De ha van saját sebessége, akkor még gyorsabban lebeg.
Ezért a folyó mentén való mozgás sebességének megállapítása érdekében ki kell egészíteni a hajó saját sebességét és sebességét.
5. probléma: A hajó saját sebessége 21 km / h, a folyó sebessége 4 km / óra. Keresse meg a hajó sebességét a folyó mentén.
Most képzeljük el, hogy a hajónak meg kell vitorláznia a folyó áramlata ellen. Motor nélkül, vagy legalábbis vidám, az áram az ellenkező irányba viszi. De ha hajóját saját sebességgel adod meg (motor indításához vagy vitorlázó leszálláshoz), az áram továbbra is visszahúzza azt, és megakadályozza, hogy a sebesség haladjon előre.
Ezért annak érdekében, hogy megtalálja a hajó sebességét az árammal szemben, az áram sebességét le kell vonni a saját sebességéből.
6. probléma: A folyó sebessége 3 km / h, a hajó sebessége 17 km / h.
Keresse meg a hajó sebességét az árammal szemben.
Probléma 7. A hajó saját sebessége 47,2 km / h, a folyó sebessége pedig 4,7 km / h. Keresse meg a hajó sebességét a jelenlegi és az aktuális áramlás mellett.
Válasz: 51,9 km / h; 42,5 km / h.
8. probléma A motorhajó sebessége az áram mentén 12,4 km / h. Keresse meg saját hajósebességét, ha a folyó sebessége 2,8 km / h.
9. probléma A hajó sebessége az árammal szemben 10,6 km / h. Keresse meg saját hajó sebességét és sebességét a lefelé, ha a folyó sebessége 2,7 km / h.
Válasz: 13,3 km / h; 16 km / h.
A sebesség az áramlás mentén és az áramerősséggel szembeni sebesség.
Bemutatjuk a következő jelölést:
Vc. - saját sebesség,
Vtech. - áramlási sebesség,
V a tech. - sebesség lefelé,
V pr.tech. - sebesség az árammal szemben.
Ezután a következő képleteket írhatjuk:
Próbáljuk meg grafikusan ábrázolni:
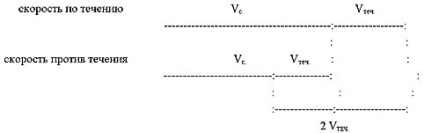
Következtetés: az áramlás mentén és az áramlással ellentétes sebesség különbsége az áramlási sebesség kétszerese.
Vno tech - Vnp. tech = 2 Vtec.
Vtech = (V az aktuális - Vnp teszten): 2
1) A hajó sebessége az árammal szemben 23 km / h, a sebesség sebessége 4 km / h.
Keresse meg a hajó sebességét a folyó mentén.
2) A motorcsónak sebessége a folyó mentén 14 km / h / perc, az áram sebessége 3 km / h. Keresse meg a hajó sebességét az árammal szemben
10. feladat: Határozza meg a sebességet és töltse ki a táblázatot: