A töltésrendszer energiája, egy magányos vezető és egy kondenzátor
1. A fixpontos díjak rendszerének energiája. Az interakció elektrosztatikus erői konzervatívak; ezért a díjak rendszere potenciális energia. Találjuk meg a potenciális energiát egy Q1 és Q2 kétpontos díjrendszerrel. egymástól távoli távolságra helyezkednek el. Mindegyik díj a másik oldalon potenciális energiával bír:
ahol # 966, 12 és Vagyis a Q2 töltés által generált potenciálokat a Q1 töltési ponton és a Q1 töltést a Q2 töltés helyén. A ponttöltés területének lehetősége:
A két díj felszámolásához ezért a Q3, Q4 díjakat. ..., láthatjuk, hogy n-in-charge díjak esetében a ponttöltések rendszerének interakciós energiája
ahol ji az a pont, ahol a Qi töltés található. minden megrendelés, kivéve i-es.
2. Egy töltött magányos vezető energiája. Legyen egy magányos vezető, amelynek töltése, kapacitása és potenciálja egyenlő Q, C, # 966; Növelje a vezető töltését dQ-val. Ehhez szükség van arra, hogy a töltés dQ-ját a végtelenektől a magányos vezetőig átvigyék, ezzel egyenlő munkát teremtetve
Ha a testet nullától potenciálig j-ra töltjük, akkor a munkát be kell fejezni
A töltött vezeték energiája megegyezik azzal a munkával, amelyet meg kell tenni a vezetõ töltéséhez:
Ezt a képletet is nyerhetjük abból a tényből, hogy a vezetõ potenciálja minden ponton megegyezõ, mivel a vezetõ felülete egyenlõtlen, feltételezve, hogy a vezetõ potenciál j, (3)
hol van a karmester töltése.
3. A feltöltött kondenzátor energiája. Mint minden töltött vezető esetében, a kondenzátornak olyan energiája van, amely a (4) képlet szerint egyenlő
ahol Q a kondenzátor töltése, C a kapacitása, a Dj a potenciálkülönbség a lemezek között.
Az (5) kifejezéssel megtalálhatjuk azt a mechanikai erőt, amellyel a kondenzátorlemezek egymást vonzzák. Ehhez tegyük fel, hogy az x távolság a lemezek között változik például a dx összeggel. Ezután a cselekvõ erõ befejezi a munkát
a rendszer potenciális energiájának csökkenése miatt
A (5) lapos kondenzátor kapacitásának pótlását megkapjuk
Egy adott energiaértékre vonatkozó differenciálódás (lásd a (6) és (7) bekezdést) származtatva megtaláljuk a szükséges erőt:
ahol a mínuszjel azt jelzi, hogy az F erő a vonzás.
4. Az elektrosztatikus mező energiája.
Transform általános képletű (5), amely kifejezi az energiát egy sík kondenzátoron díjak és a potenciálok vocpolzovavshis expressziós a kapacitás egy lapos kondenzátor (C = E0 ES / d), és az idő-felületi potenciál közötti lemezek (Dj = Ed). Aztán megkapjuk
ahol V = Sd a kondenzátor térfogata. Ez a képlet azt mutatja, hogy a kondenzátor energiája az elektrosztatikus mezőt jellemző mennyiséggel, az E intenzitással fejeződik ki.
Az elektrosztatikus mező ömlesztett energiasűrűsége (egységnyi térfogat energia)
Ez a kifejezés csak egy izotróp dielektrikumra érvényes, amelyre a következő összefüggés érvényes: P = ce0 E.
Az (5) és (8) képletek összekötik a kondenzátor energiáját egy sorozattal a lemezeken és a mező intenzitásával. Természetesen felmerül a kérdés az elektrosztatikus energia lokalizációjáról, és mi az a hordozó töltés vagy ion? E kérdésre csak a tapasztalat adható meg. Az elektrosztatika vizsgálja az állandó töltések időállandó mezőit, azaz azokat a mezőket és díjakat, amelyek meghatározzák őket, elválaszthatatlanok egymástól. Így az elektrosztatika nem válaszolhat a feltett kérdésekre. További fejlesztés az elmélet és a kísérlet azt mutatta, hogy az időben változó elektromos és mágneses mezők létezhetnek autonóm-helyen való tekintet díjak izgatott és szaporodni a térben elektromágneses hullámok, spo, akik képesek átvinni az energiát. Ez meggyőzte-CIÓ megerősíti a alaphelyzetét rövid hatótávolságú elmélet lokalizációja energia az energia területén, és hogy a hordozó egy területen.
Két egyenlő díja az ellenkező jelből, + Q és -Q, egymástól l távolságra helyezkedve, elektromos dipólust képez. A Ql mennyiséget a dipólus pillanatnak nevezzük, és a p szimbólum jelöli. Sok molekula egy dipólus pillanat, például egy diatomás CO molekula (a C atomnak van egy kis pozitív töltése, és O kis negatív töltéssel rendelkezik); Annak ellenére, hogy a molekula egésze semleges, a töltés elválasztása a két atom közötti egyenlőtlen eloszlás miatt következik be. (A szimmetrikus diatomi molekulák, mint például az O2, nem rendelkeznek dipólus pillanattal.)
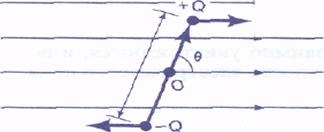
Először vegyünk egy dipólust egy pillanatra # 961; = Ql, amelyet az erősséggel homogén elektromos mezőbe helyezett # 917;. A dipólus momentumot egy v vektor formájában ábrázolhatjuk, amely abszolút nagyságrendben Ql-re változik, és a negatív töltésnek a pozitív töltés felé irányul. Ha a mező egyenletes, akkor a pozitív töltésen, a QE-n és a negatív QE-ben fellépő erők nem hoznak létre a dipólusra ható erőt. Mindazonáltal egy forgó pillanat megjelenéséhez vezetnek, amelynek nagysága az O dipólus középpontjához viszonyítva
vagy vektorrekordban
Ennek eredményeképpen a dipólus elfordul, úgyhogy a p vektor párhuzamos az E-rel. A W munkát a dipólus feletti elektromos mező hajtja végre, amikor a szög # 952; változik q1-ről q2-re. megadja
Az elektromos tér által végzett munka eredményeképpen a dipólus U energia potenciálja csökken; ha U = 0-t állítunk be, amikor p ^ # 917; (# 952; = 90 0), majd
U = -W = - pEcos # 952; = - p · # 917;.
Ha az elektromos mező nem egységes, az erők jogszabály-nek a pozitív és negatív töltések dipól lehet egyenlőtlen nagyságú, majd egy dipólus, amellett, hogy a nyomaték, cselekszik és az eredő erő.
Tehát mi látjuk, mi történik egy villamos dipólal, amelyet egy külső elektromos mezőbe helyeznek. Most forduljunk az ügy másik oldalára.
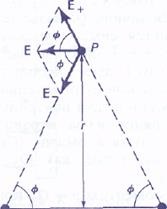
Ábra. Elektromos mező, amelyet egy elektromos dipólus hoz létre.
Tegyük fel, hogy nincs külső mező, és meghatározzuk a dipólus által létrehozott elektromos mezőt (amely más díjakra is képes). Az egyszerűség kedvéért csak a dipólus közepére merőleges pontokra korlátozódunk, mint a pont # 929; ábrán. r távolságon belül helyezkedik el a dipólus közepétől. (Ne feledje, hogy az ábrán nem az egyes töltések távolsága P-re, azaz (r 2 + / 2/4) 1/2.) Az elektromos mező erőssége a ponton # 929; jelentése
ahol E + és E az egymásnak abszolút értékkel egyenlően pozitív és negatív töltések által előállított mezőintenzitások:
Az y-komponensük a ponton # 929; kölcsönösen megsemmisült, és abszolút nagyságrendben az elektromos térerősséget # 917; jelentése
[a dipólus közepére merőleges irányban].
A dipólustól (r> /) távolabb ez a kifejezés egyszerűbb:
[a dipólus közepére merőlegesen, r >> l] esetén.
Látható, hogy a dipólikus elektromos tér erőssége gyorsabban csökken, mint egy ponttöltésnél (pl. 1 / r 3 az 1 / r 2 helyett). Ez várható: nagy távolságra, két ellentétes jelzőtábla úgy tűnik olyan közel, hogy semlegesítik egymást. Az 1 / r3 forma függvénye olyan pontokra is érvényes, amelyek nem fekszenek a merőlegesre a dipólus közepére.