A görbe közelítése (zaj és csúcskiegyenlítés egy soros sorozatban) - verem túlcsordulása oroszul
A valódi számok egydimenziós tömbje (több ezer elem). Ha ezeket az értékeket ábrázoljuk, láthatjuk, hogy az értékek bizonyos ingadozása (elterjedése) (néhány éles csúcsú).
Példa (az egyértelműség érdekében a mérési intervallumok egyenletesek):
- Hőmérsékleti értékek
- Fényszint
- Akkumulátor töltés
- A folyadék szintje
- és így tovább.
ref. 10 12 15 40 17 16 12 10 22 12 14 15 14 10 12
simított.
10 13 15 16 16 14 12 16 14 13 14 14 13 11 12
Nem szükséges növelni a pontok számát, hogy kiegyenlítsük a leolvasásokat:
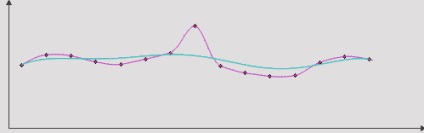
(durva vázlat: "simított vonal" - hirtelen ugrások nélküli leolvasások)
Nyilvánvaló, hogy ez szükségessé teszi az adatok közelítését, de néhány napig nehézséget okoz az algoritmus megadása a Bezier-görbe közelítéséhez a szükséges formához:
ahol p1 a szomszédok két szomszédja közötti simított közbenső érték, t = 0.5 (az ötlet szerint pontosan 0,5, hogy a köztes értéket kell venni).
Aztán megtaláltam az algoritmust. és ő maga is itt fekszik.
De ez az algoritmus nem megfelelő, mert legfeljebb 32 pontban dolgozunk, és a tényekkel együtt túl sokáig tart a JS-nél, ha egyáltalán. És írja le az algoritmust tényezők nélkül (ez lehetséges, ha úgy gondolja, hogy a képletek a Wikipédiából), nem tudom.
Használhatja az általam megadott formulát is, és egymás után járni, de nem hiszem, hogy ez jó ötlet. Ha egyszerre több mint 32 pontot használhat (legalább 100 pontot), akkor szórakoztatóbb lenne. De nem tudom, hogyan kell leírni azt a képletet, amellyel írni akarom az algoritmust.
Tudja-e valaki, hogy a numerikus sorozatban a "zaj" és a "csúcsok" ki fog simulni?
Egy nappal többet fogok harcolni, de valami kiderül, hogy az algoritmussal kerül meghatározásra.
Nem vagyok nagyon matematika, tehát nem tudom átjutni az elméleten a képletre.
Remélem, valaki segít nekem ezzel.
Megpróbáltam használni a "mozgó átlagot" (a llama tanácsa alapján), de az adatok nagyon torzultak. Itt van a kód (nem úgy tűnik, hogy van, de ki tudja):
De ennek eredményeképpen mindenképpen megálltam a kezdeti változatban - a Bezier simításával (négyzetes görbe):
A 4-réses szakaszok kielégítő eredményt adnak.
PS Ha nincs jobb lehetőség, akkor maradok ezen a lehetőségen.
Nézd, én kitaláltam: