Ohm törvénye
A modern világban az elektronikus technológiát ugrásszerűen fejlesztik. Minden nap van valami új, és nemcsak a meglévő modellek kis javulása, hanem az olyan innovatív technológiák alkalmazása is, amelyek lehetővé teszik a jellemzők többszörös javítását.
Nem messze az elektronika és a műszer iparhoz - sőt fejleszteni és kiadja az új eszközök piacán, meg kell alaposan tesztelni kell, mind a szakaszában tervezés és fejlesztés, valamint a termelési fázisban. Új mérési technikák és új mérési módszerek, következésképpen új kifejezések és fogalmak vannak.
Azok számára, akik gyakran szembesülnek érthetetlen rövidítéseket, rövidítéseket és kifejezéseket, és mélyebben meg akarják érteni a jelentésüket, és ez a címsor célja.
Az Ohm törvénye olyan fizikai törvény, amely meghatározza a forrás elektromotoros erejének vagy az elektromos feszültségnek az áramerősségével és a vezető ellenállásával való kapcsolatát. Kísérletileg 1826-ban telepítették, és felfedezték Georg Oma felfedezőjét.
Itt X a galvanométer jelzése, vagyis az aktuális jelölésnél az aktuális I. a - a mennyiség jellemző tulajdonságait egy áramforrás állandó széles tartományban és független az az áram nagyságának, vagyis a jelenlegi terminológia elektromotoros erő (EMF), l - meghatározott érték hosszú összekötő vezetékek, amelyek a modern reprezentációk megfelel a ellenállása a külső áramkörben R, és végül b paraméter jellemző tulajdonságait az egész rendszer, ami most már lehetséges, hogy a belső számviteli áramforrás ellenállás r.
Ohm törvénye a teljes láncra:
- - EMF feszültségforrás (V),
- - áramerősség az áramkörben (A),
- - minden külső áramkör elemének (Ohm) ellenállása,
- - a feszültségforrás belső ellenállása (Ohm).
Ohm törvényéből a teljes láncra következnek a következmények:
- Amikor r<
- Az r >> R esetében az áramerősség nem függ a külső áramkör tulajdonságaitól (a terhelés nagyságától). És a forrást nevezhetjük áramforrásnak.
(ahol a feszültség vagy feszültség csökken, vagy ami ugyanaz, a potenciális különbség a vezetékszakasz eleje és vége között) szintén az "ohm törvény" -nek nevezzük.
Így a zárt áramkörben lévő elektromotoros erő, amelyen keresztül a (2) és (3) szerint áramlik, egyenlő:
Ez azt jelenti, hogy a feszültség csökkenése az áramforrás belső ellenállása és a külső áramkör esetében megegyezik az EMF forrásával. Ebben az egyenletben az utolsó kifejezést "terminál feszültségnek" hívják, mert azt egy voltmérő jelzi, amely a forrás feszültségét a hozzá csatlakoztatott zárt áramkör kezdete és vége között mérik. Ebben az esetben mindig kevesebb, mint az EMF.
A (3) képlet másik bejegyzéséhez, nevezetesen:
Egy másik megfogalmazás érvényes:
Az áramkör áramköre közvetlenül arányos a feszültséggel, és fordítottan arányos az áramkör ezen szakaszának elektromos ellenállásával.
Az (5) kifejezést újraírhatjuk:
ahol a G arányossági tényező a vezetőképesség vagy elektromos vezetőképesség. Kezdetben a vezetőképesség mérési egysége "fordított Om" - Mo volt, ezt követően átnevezték a Siemens (megjelölés: See S).
Mnemonikus diagram a törvényhez

Az Ohm törvényének három összetevőjét ábrázoló diagram
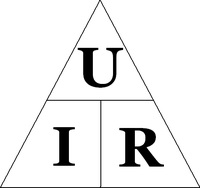
Egy diagram, amely segít megemlíteni az Ohm törvényét. Szükséges a szükséges érték bezárása, és két másik szimbólum megadja a képletet a számításhoz
Ennek a diagramnak megfelelően a következő kifejezés formálisan írható:
Amely csak számunkra tud kiszámolni (egy ismert áramra hivatkozva, amely ismert feszültséget hoz létre az áramkör adott szakaszán), ennek a szakasznak az ellenállását. De egy matematikailag helyes kijelentés, hogy a vezető ellenállása egyenesen arányos a rá alkalmazott feszültséggel, és fordítottan arányos a folyó áramlással, fizikailag hamis.
Különlegesen meghatározott esetekben az ellenállás ezeknek az értékeknek a függvénye, de alapértelmezés szerint csak a vezető fizikai és geometriai paraméterei határozzák meg:
- - az anyag rezisztenciája, amelyből a vezetõ készült,
- - hossza
- Keresztmetszete
Ohm törvényét és az erőátviteli vonalakat
Az erőátviteli vonalak (LEP) egyik legfontosabb követelménye a veszteségek csökkentése, amikor energiát adnak a fogyasztónak. Ezek a veszteségek most a vezetékek fűtését jelentik, vagyis az áram energiáját hőenergiává változtatják, amelyért a vezetékek ohmos ellenállása felelős. Más szóval, a feladat az, hogy az áramforrás lehető legnagyobb részét a fogyasztónak = az átviteli vonal minimális teljesítményveszteséggel = =. ahol és ezúttal a vezetékek teljes ellenállása és a generátor belső ellenállása van (ez utóbbi még mindig kisebb, mint az átviteli vonal ellenállása).
Ebben az esetben a teljesítményveszteséget a következő kifejezés határozza meg:
Ebből következik, hogy egy állandó átviteli teljesítménynél a veszteségek közvetlenül növekednek az átviteli vonal hosszával arányban, és fordítottan arányosak az emf négyzetével. Ezért kívánatos minden irányban növelni, amit a generátor tekercselésének elektromos ereje korlátoz. És a feszültség növelése a vonal bemeneténél már a generátor áramának kimenete után következik, ami probléma az egyenáramra. Azonban a váltakozó áramra vonatkozóan ez a feladat sokkal könnyebb megoldást találni a transzformátorok használatával, amelyek előre meghatározzák a váltakozó áramú átviteli vonalak elterjedését. Azonban, ha a feszültség megnövekedett, korona veszteség keletkezik, és nehézségek merülnek fel a földfelszínről való elszigetelés megbízhatóságának biztosításában. Ezért a legnagyobb, gyakorlatilag használt feszültség a hosszú távú villamos vezetékben nem haladja meg az egymilliót.
Ezen felül, minden vezető, amint J. Maxwell, a jelenlegi változás neki, energiát sugároz a környező térbe, ezért távvezeték viselkedik, mint egy antenna, ami bizonyos esetekben együtt ohmos veszteségek figyelembe veszi és sugárzási veszteség.
Az Ohm-törvény differenciált formában
Az ellenállás függ az áramtól folyó anyagtól és a vezető geometriai méreteitől is.
Hasznos az Ohm törvényének átírása az úgynevezett differenciált formában, amelyben eltűnik a geometriai dimenzióktól való függés, majd az Ohm törvénye kizárólag az anyag elektromos vezető tulajdonságait írja le. Az izotróp anyagok esetében:
- - áramsűrűség vektor,
- - vezetőképesség,
- - az elektromos térerősség vektora.
Az ebben az egyenletben szereplő összes mennyiség a koordináták és általában az idő függvénye. Ha az anyag anizotróp, az aktuális sűrűség és intenzitás vektorok irányai nem egyezhetnek meg. Ebben az esetben a vezetőképesség egy rangsori tenzor (1, 1).
A fizika szakasza, amely az áramlást különböző médiumokban vizsgálja, a folyamatos média elektrodinamikájának nevezik.
Ohm-törvény a váltakozó áramra
Az áramkörök tulajdonságaira vonatkozó fenti megfontolások érvényben maradnak egy forrás (generátor) időváltozó EMF használatakor. Különös figyelmet kell fordítani arra, hogy figyelembe vegyék a fogyasztó sajátos tulajdonságait, ami a maximális értékek elérésének túlfeszültsége, azaz a fáziseltolódás figyelembevétele.
Ha az áram szinuszos, ciklikus frekvenciával rendelkezik, és az áramkör nemcsak aktív, hanem reaktív komponenseket is tartalmaz (kapacitások, induktivitás), az Ohm-törvény általános; a belépő mennyiségek összetettekké válnak:
- U = U 0ei ωt a feszültség vagy potenciálkülönbség,
- Én vagyok az áramerősség,
- Z = Re -i δ - komplex impedancia (impedancia),
- R = (Ra 2 + Rr 2) 1/2 az impedancia,
- Rr = ωL - 1 / (ωC) - reaktancia (az induktív és a kapacitív különbség),
- Ra egy aktív (ohmikus) ellenállás, független a frekvenciától,
- δ = - arctg (Rr / Ra) - fázisváltás a feszültség és az áramerősség között.
Az átmenet a komplex változó az áram és feszültség értékek a tényleges (mért) értékek állíthatók elő azáltal, hogy a vélt vagy valós része (de minden eleme a lánc ugyanaz!) A komplex értékek ilyen mennyiségben. Ennek megfelelően, a fordított átmenetet van kiképezve, például úgy, hogy a kiválasztási Ezután az összes értékeit áramok és feszültségek az áramkörben kell tekinteni
Ha az áram időben változik, de nem szinuszos (vagy akár időszakos), akkor a szinuszos Fourier komponensek összegeként is megjeleníthető. Lineáris láncok esetében az áram Fourier-expanziójának komponensei függetlenül működnek.
Azt is meg kell jegyeznünk, hogy az Ohm törvénye csak a legegyszerűbb megközelítés az áram függésének a potenciális különbségre és az ellenállásra történő leírásából, és bizonyos struktúrák csak szűk értéktartományokban érvényesek. Bonyolultabb (nemlineáris) rendszerek leírására, amikor az ellenállás függését az aktuális erősségtől nem lehet figyelmen kívül hagyni, szokásos az áramfeszültség jellemzőinek megvitatása. Az Ohm-törvénytől való eltérések is megfigyelhetők olyan esetekben, amikor az elektromos mező változása olyan nagy, hogy nem lehet figyelmen kívül hagyni a töltőhordozók tehetetlenségét.
Ohm törvényének értelmezése
Az ohm törvényét egyszerűen a drude-elmélet magyarázza:
- - elektromos vezetőképesség
- - elektronkoncentráció
- - elemi díj
- - a relaxációs idő a momentum (az idő, amikor az elektron "elfelejti", hogy melyik irányban mozog)
- Az elektron tényleges tömege