Elhasználódási fáradékonysági görbe
Fáradtság, fáradási görbe anyagvizsgálata (Veler görbe)
Fáradtság, fáradási görbe anyagvizsgálata (Veler görbe)
A fáradási görbe (a Veler-görbe) egy olyan terhelés, melynek során az anyag egy adott számú terhelési ciklussal megsemmisül, e ciklusok számából. A fáradási görbe (a Veler görbe) a vizsgálat eredménye.
A tiszta hajlítás szimmetrikus ciklusának leggyakoribb vizsgálata. mivel ez a stresszciklus az anyag számára legveszélyesebb, és egy kísérlet végrehajtása egyszerűbb, mint más típusú ciklusokhoz.
A kísérlethez 6-10 teljesen azonos mintát állítunk elő, amelynek szigorúan kör alakú henger alakja van a munkadarabon belül. A minták átmérője általában 5-10 mm.
Az első mintát úgy terheljük meg, hogy a benne megjelenő maximális normál feszültségek minden bizonnyal alatta maradjanak az anyag végső szilárdságának (), de az állóképességi határ fölött. A későbbi minták esetében a maximális feszültség csökken.
A fordulatszámmérő jelen a teszt gép, fix terhelési ciklusok számának, amely támogatja mindegyik mintából, amíg hiba. Szerint a vizsgálati eredményeket grafikusan ábrázoltuk a ciklusok számát (N), amely fenntartja a minta törés nélküli, a maximális feszültség () a mintában keletkezett (ábra. 14.3).
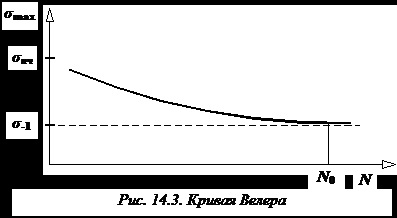
A 14.3 ábrán látható, hogy a szám csökkenése után az (N) ciklusok száma nagyon gyorsan növekszik, így a fáradási görbe jelentős hosszúságú az abszcissza tengely mentén. Sok anyag esetében a fáradási görbe aszimptotikusan megközelíti a maximális stressz bizonyos értékét, amelyből a minták nem mutatnak kudarcot. Ezért, ha egy megfelelő vizsgálati ciklusok számát lehet állítani.
A gyakorlat azt mutatja, hogy a ciklusok megsemmisülése nélkül túlélő minták korlátlan ideig működhetnek (például a vasúti autó tengelye Moszkvából Vladivostokba a ciklusok tapasztalataira).
A kimerültségi teszt adatbázis () a fáradtság tesztjének előre meghatározott maximális hossza.
A ciklus legnagyobb stresszét, amelynél a fáradtság meghibásodása nem következik be a vizsgálati bázis előtt, az állóképességi határnak nevezik.
A színes anyagok fáradási görbéi nem rendelkeznek aszimptotommal, és rendszereik nullára esnek, amikor N nő. A nemvas anyagok esetében bevezetik a feltételes kitartásra vonatkozó határérték fogalmát. A feltételes kitartás határértéke esetén a maximális stresszt feltételezzük, amelynél a minta legalább a ciklusoknak ellenáll.