Normál forgalmazási jog - stadopedia
A folyamatos, véletlenszerű változót a szokásos törvény szerint osztják szét. ha eloszlási sűrűsége a következő:
A normál eloszlás sűrűségének grafikont normális görbének nevezik (Gaussian görbe). Vizsgáljuk meg a függvényt (24.1).
1) A függvény meghatározásának területe: (-∞, + ∞).
2) f (x)> 0 minden x-hez (tehát az egész gráf az Ox tengely felett van).
3) vagyis az Ox tengely a grafikon vízszintes aszimptotikája
4) x = a esetén; x> a esetén. x-nél 5) F (x - a) = f (a - x), azaz a grafikon szimmetrikus az x = a egyenes vonalhoz képest. 6) mikor. azaz a pontok az inflexiós pontok. Egy rendes eloszlású véletlen változó matematikai elvárásainak kiszámításához használjuk azt a tényt, hogy a Poisson integrál. (az első kifejezés egyenlő 0-val, mivel az integrand páratlan, az integráció határai szimmetrikusak a nullához képest). Következésképpen a normál eloszlás paraméterei (a és # 963; ) megegyeznek az adott véletlen változó matematikai elvárásával és átlagos négyszöges eltérésével. Az ábrán a Gaussian görbék közelítő nézete látható a különböző paraméterértékekre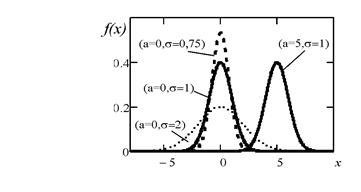
Nézzük meg az elosztási funkció formáját a normális törvények szerint:
A (24.2) integrál nem fejezhető ki az elemi funkciók tekintetében. Ezért az F (x) értékek kiszámításához táblázatokat kell használnunk. Azért íródnak, ha a = 0, és # 963; = 1 (normalizált eloszlás), azaz a funkcióhoz
A paraméterek tetszőleges értékeire normalizált eloszlású véletlen változó eloszlásfüggvényét a Laplace függvényben lehet kifejezni, ha a helyettesítést végrehajtjuk:. akkor. (24,4)
És egy normális eloszlású véletlen változó valószínűsége egy adott intervallumra esik:
Megjegyzés. Ha táblázatos Laplace funkciót használ. akkor szem előtt kell tartani.
Egy példa. Az X véletlen változó normál eloszlású a = 3 paraméterekkel, # 963; = 2. Keresse meg annak valószínűségét, hogy értéket kap az intervallumtól (4, 8).