Mátrixok, kiegészítés, kivonás, szorzás

1) Az első fellépés. Egy mínusz mátrix kimenete (mínusz mátrixba való belépés).
A mátrixon túlmutatunk egy mínuszon, a mátrixjel minden eleméről:

Bevezetünk egy mínuszt a mátrixban, megváltoztatva az egyes mátrix elemek jeleit.

2) A második akció. Egy mátrix szorzása egy számmal.

Az egyetlen dolog, ami ebben a példában kívánatos, hogy mínuszot adjon a mátrixhoz: De ha a mátrix minden elemét a maradék nélkül 7 osztja el. akkor lehetséges (és szükséges!) meg kell osztani.

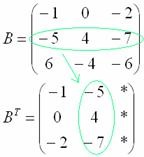
3) A harmadik cselekvés. A mátrix átültetése.

Ezután a második oszlopban átírjuk a második sort:

4) A negyedik cselekvés. A mátrixok összege (különbség).

NEM MINDEN MÉRETEK LEHETŐSÉGEN MŰKÖDIK. A mátrixok hozzáadásának (kivonásának) elvégzése érdekében szükséges, hogy azok azonos méretűek legyenek.

Az ötödik fellépés. Mátrixok szorzása

Ha egy mátrixot meg kell szorozni mátrixszal, akkor szükséges, hogy a mátrix oszlopainak száma megegyezzen a mátrix sorainak számával.

- Próbálja meg azonnal elkapni a törvényt.

Szorzózzuk meg a mátrixot mátrix szerint

Kérjük, vegye figyelembe, hogy! Ez majdnem mindig ilyen!

Így, amikor szaporodsz, nem tudod átrendezni a mátrixokat!

Determinánsok, tulajdonságok, algebrai kiegészítők, számítások

Megnevezések. Ha mátrix van megadva. akkor determinánsát jelölik. Szorosan a meghatározó tényezőt latin betű vagy görög is jelöli.

Tehát a "három-három" determináns három kis determináns megoldására van redukálva, vagy ahogy hívják, a MINOR. Az a kifejezés, amelyet emlékeznem kell, ráadásul emlékezetes: a kiskorú kicsi.

Mivel a meghatározó módszert az első sorra kiterjeszti. nyilvánvaló, hogy minden körülötte:

1) A jelek mátrixából kiírjuk a megfelelő jelet:

2) Aztán írjuk le az elemet:

3) TALÁLHATÓBB, töröljük a sor és oszlop, amelyben az első elem áll:

A fennmaradó négy szám két-két-két meghatározót alkot, amelyet ennek az elemnek (egységeknek) MINOR-nak neveznek.

Átmegyünk a vonal második eleméhez.

4) A jelek mátrixából kiírjuk a megfelelő jelet:

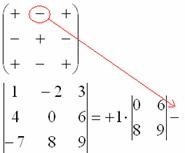
5) Ezután írja be a második elemet:

6) KÉRELEM, töröljük a sor és oszlop, amelyben a második elem áll:

A fennmaradó négy számot egy kis azonosítóban írják.

Nos, az első sor harmadik eleme. Nem eredeti:

7) A jelek mátrixából levonjuk a megfelelő jelet:

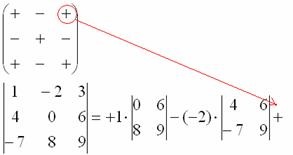
8) Megjegyezzük a harmadik elemet:

9) TALÁLHATÓBB, töröljük a sor és oszlop, amelyben a harmadik elem áll:

1. A meghatározó nyereségesebb a TOI vonal (oszlop) megnyitásakor, ahol:

Ebből következik egy fontos tény: a determináns sorai és oszlopai egyenlőek.

2. Ha a determináns két sorát (vagy két oszlopát) kicseréljük,
akkor a determináns megváltozik

Ez azt jelenti, hogy a sorok (oszlopok) bármely pár átrendeződése megváltoztatja a determináns jeleit az ellenkező irányba.

3. A determináns sorából (oszlopából) közös tényezőt lehet létrehozni

Az ellenkezője is igaz: a szorzót nem csak elvégezni, hanem be is vezetni. és a meghatározó bármelyik sorában vagy bármelyik oszlopában.

4. Ha a meghatározó két sor (oszlopa) arányos
(mint egy speciális eset - ugyanaz), akkor ez a determináns nulla

A nulla sor (oszlop) meghatározója nulla

Milyen meghatározó tényezők hasznosak a tudáshoz?

1) A determináns értéke nem változik az átültetés során. Az ingatlant megtanulják.

2) A sorok (oszlopok) páronkénti permutációja megváltoztatja a determináns jeleit az ellenkezőjére. Emlékezzünk az ingatlanra is, és próbáljuk elkerülni a zavart.

3) A meghatározó sorából (oszlopából) a szorzót (és visszaadhatja). Használjuk, ahol nyereséges.

Ha a determináns sorai (oszlopai) arányosak, akkor nulla. A nulla sor (oszlop) meghatározója nulla.

A lineáris egyenletek rendszere Cramer tétele

Lineáris egyenletek rögzítési rendszerei mátrix formában