Másodrendű felületek kialakítása a mathcad környezetben
Felületek építése Mathcadban.
A Mathcad rendszer felületrajzának megalkotása többféle módon történhet.
1 Felületek felépítése a pályázók mátrixával.
Mivel a mátrix elemeinek M - indexelt változókat egész szám in-Dex létrehozása előtt a mátrix kell állítani indexek egy rangsorolt NE-öv egész értékek, majd tőlük egy rácsot képeznek értékek x és y - koordinátáit z-z (x, y) . Az x és y értékek lehetnek valódi számok.
A fenti definíciók után egy grafikus sablon kerül beírásra (akár a Beszúrás menü almenüjében, akár a Grafikus panel segítségével). A sablon bal felső sarkában található a kurzor helyén. A sablon egyetlen belépési pontot tartalmaz - egy sötét téglalapot a fő sablon bal alsó sarkában. Ebben a mezőben meg kell adnia a mátrix felületi applikátor nevét. Ezt követően be kell állítania az egérmutatót a grafikus blokkról, és kattintson a bal gombbal.
Meg kell jegyezni, mint egy grafikon alapján a mátrix, amely csak a koordinátákat magasságú figura, a valós mértékét tengelyeinek abszcisszák és ordináta ismeretlen, és nem szerepel az ábrán. Azonban lehetőség van arra, hogy a mátrixelemek rendszámait egy adott irányba vezesse. Ügyelni kell arra, hogy generálja a vektorok X és Y, hogy vizsgálja meg a természetes felszíni és látható volt kívánt darabok felületét.
2 A háromdimenziós grafikonok összeállítása mátrix meghatározása nélkül.
Ebben az esetben az építéshez elegendő az x és y változók funkciójának meghatározása. Ennek eredményeként a felületek grafikonjainak elkészítése is egyszerű, valamint a kétdimenziós grafikonok kialakítása. Az ilyen konstrukció hátrányai a skálázás bizonytalansága és az a tény, hogy a második rend minden felületét nem lehet ilyen módon felépíteni.
Háromdimenziós grafikonok formázása.
A háromdimenziós diagramok formázásának elve megegyezik a kétdimenziós diagramok formázásával. Az egyetlen különbség több formázási lehetőség.
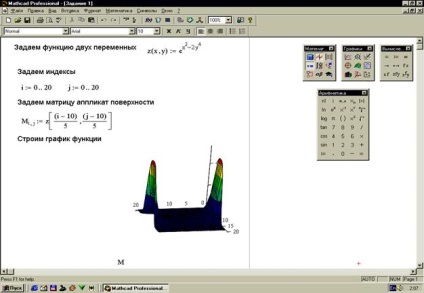
1. feladat: A felszínt a pontok felhordójának mátrixa mentén kell felépíteni (30. ábra).
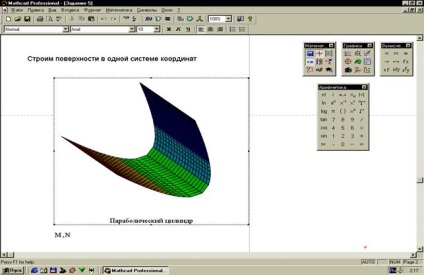
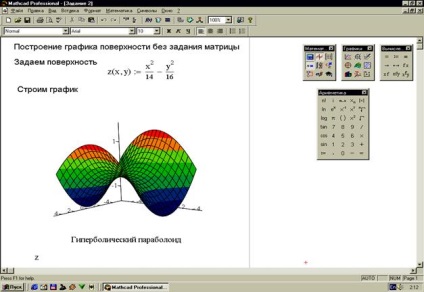
2. feladat: Hozzon létre egy felületet mátrix meghatározása nélkül (31. ábra).
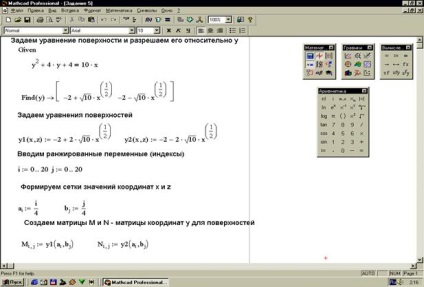
A felszíni egyenletet nem mindig határozza meg kifejezetten. Annak érdekében, hogy egy adott felületet implicit módon felépítsünk, először meg kell oldanunk egy adott felület egyenletét egy változó vonatkozásában, majd a kapott egyenletből a felületeket felépítenünk.
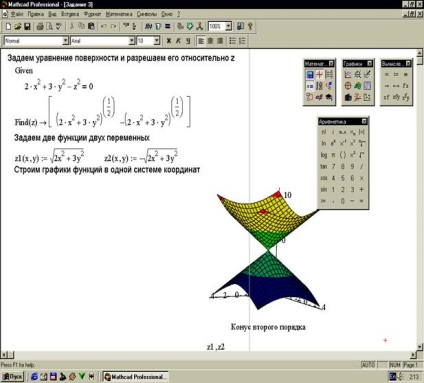
3. feladat: Az egyenlet által meghatározott felületet (32. ábra).
4. feladat: Az egyenlet által meghatározott felületet (33. ábra).
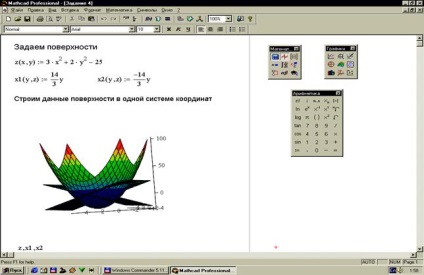
A Mathcad rendszer képességei lehetővé teszik, hogy egymással metsző felületeket építsenek össze egy koordináta rendszerben.
Feladat 5. Felületek felépítése. (34. ábra).
A Mathcad csomagban paraméteres formában definiált felületek is létrehozhatók. Ilyen konstrukciók példáit a 36. és 37. ábrák mutatják be.