Know-how, előadás, numerikus integráció
Kivonat: Az interpoláció tipus-téglalapok, trapézok, Simpsons legegyszerűbb kvadratúra-formuláit tanulmányozzák. A képletek valós hibájának becslésére Runge szabályt használnak. A Gauss-kvadratúra-képlet fogalmát adjuk meg. A többdimenziós integrálok kiszámításának módszereit figyelembe veszik.
Ebben az előadásban figyelembe fogjuk venni a numerikus integráció problémáját. Az egyik változó funkcióinak numerikus integrálására szolgáló képleteket kvadratúra-képletnek nevezzük. A meghatározott integrál (egy szegmens vagy többdimenziós tartomány) megközelítő számításának problémája valójában két független alfejezetre oszlik. Az első egy táblázatos funkció integrálása (például egy laboratóriumi kísérletben). Ebben az esetben nincs a priori információ az integrandus simaságáról, és az integrációs csomópontok kiválasztásának lehetőségei nagyon korlátozottak. Erre a problémára a leghatékonyabb az interpolációs típus kvadratúra-képlete és a Runge-hiba becslés szabálya.
A második feladat az ismert függvény egy meghatározott integrál értékének kiszámítása. Ebben az esetben a számítástechnika szempontjából a legtöbb erőforrás-igényes művelet a funkció értékének kiszámítása. Kívánatos egy olyan numerikus módszer kidolgozása, amely lehetővé teszi a lehető legkisebb pontosság elérését a számítások legkisebb számával, míg a kvadratúra-képletek csomópontjainak kiválasztása teljesen a számológép kezében van. Ebben az esetben a leghatékonyabb a Gauss típusú kvadratúra-képlet.
7.1. Interpolációs kvadratúra-formulák (Newton-Cotes-képletek)
A legegyszerűbb kvadratúra-képlet (numerikus integráció képlet) a következőképpen állítható elő. Szükséges az integrál kiszámítása
Tegyük fel, hogy az f (t) nem változik () a vizsgált [a, b] intervallumon. Akkor Ha
akkor megkapjuk a négyszögek képletét egy központi ponttal
Természetesen a állandói a fenti képlet pontos - mondjuk épült kvadratúra- formula pontos lesz a polinomot lehet 0. Könnyen bizonyítani, hogy a tápszer és a középpont a téglalap nem ad pontos értéket abban az esetben egy lineáris függvény. Minden más funkciónál a ez a képlet tekinthető hozzávetőleges.
Feltételezve, hogy az f (t) intervallumban az integráció [a, b] elegendően közel lineárisak, lehetőség van helyettesíteni a közelítő értéke az integrál i terület egy trapéz, amelynek magassága (b - a) és a bázisok F (a) és f (b). Ezután a trapéz alakot kapjuk
Az általános esetekben a kvadratúra-képleteket úgy kapjuk meg, hogy az interpolációs polinom integrálódik. Az így kapott kvadratúra-képletek családját interpolációs típusú formuláknak (Newton-Cotes-formula) nevezzük.
Bevezetünk egy rácsot az integráció intervallumára, definiáljuk a függvény értékét a rács csomópontjain. A csomópontokat a kvadratúra-képlet (vagy kvadratúra) csomópontjainak nevezzük. Tegyük fel, hogy az interpolációs probléma, mint például a csomópontok halmaza, legyen az [tk. tk + 1] néha elemi szegmensnek nevezzük.
Az integrát az interpolációs polinommal helyettesítjük Lagrange formájában. Ezt feltételezzük
Vegyünk néhány konkrét esetet.
A trapéz alakja. A [tk. tk + 1] az integrátot az első fokú interpolációs polinommal helyettesítjük:
miután az elemi időintervallumon át történő integrálás után az integrál hozzávetőleges értékét kapjuk a [tk. tk + 1]:
Miután összegeztük az integrálokat az összes elemi intervallumon [tk. tk + 1] a trapéz képletet kapjuk az [a, b] intervallumhoz:
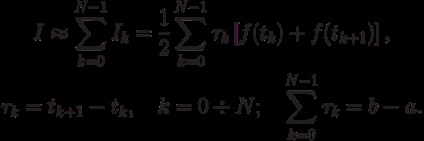
Az egyenletes rácson (egyenlő távolságra lévő csomópontokkal ellátott rács) a kapott képlet a forma