Kettős konverziós wikipédia
A projektív sík fő tulajdonsága a pontok és vonalak által definiált definíciókban és tételekben játszott szerepek "szimmetriája", és a kettősség a fogalom formalizálása. E dualitásnak két megközelítése van: a nyelvhasználatot (lásd a "dualitás elvet" alább), és egy másik, funkcionálisabb megközelítést. Teljesen egyenértékűek, mindkettő a geometria axiomatikus változatainak kiindulópontjaként szolgál. A funkcionális megközelítésben létezik a geometriai összefüggés, amelyet dualitásnak neveznek. Különös példákkal sokféleképpen lehet ilyen összefüggést kialakítani. A sík dualitásának koncepciója egyszerűen kiterjed a kettősségre minden véges dimenziós projektív geometriában.
A dualitás elve [. ]
Ha meghatározzuk a projektív sík beesési axiomatically szerkezetét tekintve ponthalmaz P. sor vonalak L és bináris reláció előfordulása I. meghatározza, hogy mely ponton át egyenes vonalak, amelyek lehetséges, hogy határozza meg a kettős síkon szerkezetét.
Ha kicseréli a "pontok" és a "vonalak" szerepét az incidencia szerkezetében
kettős struktúrát kapunk
ahol I * az I-hez képest fordított összefüggés. C * szintén egy projektív sík, amelyet a kettős (kettős) síknak hívunk C-nek.
Ha C és C * isomorf, akkor C-nek nevezik az önmagával kettős. A PG (2, K) projektív síkok bármelyik mezőre (vagy általánosabban minden olyan szakaszra, amelyik izomorf a kettős), K kettős kettős. Különösen a véges sorrend síkja mindig önmagát kettős. Azonban a nem diszkont repülőgépek között léteznek mind az önálló kettős (például a Hughes-síkok [en]), és nem az önálló kettős (például Hall-síkok).
A projektív sík nyilatkozatot pontot, repülőgépek és azok előfordulási nyert másik ilyen jóváhagyást cseréje a „pont” és „vonal” (a változás, ha szükséges, nyelvtan) az úgynevezett duális állítás. A kettős állítás, hogy "Két egyenes vonal áthalad egy egyenesen", "Két egyenes metszi egy ponton". A kettős állítás kialakulását az állítás kettősítésének nevezik.
Ha a deklaráció igaz a C projektív síkban, akkor a kettős állításnak igaznak kell lennie a kettős síkban C *. Ez abból a tényből következik, hogy a "C" bizonyíték minden egyes állításának kettőspontosítása a "C * -ban" bizonyítékot ad.
A sík dualitásának elve azt mondja, hogy az önharmonika kettős projektív síkban lévő bármely tétel dualizálása C egy másik valós tételt generál C-ban.
Ez a koncepció általánosíthatja a háromdimenziós tér dualitását, ahol a "pontok" és a "síkok" fogalmai megváltoztatják a szerepeket (és a vonalak egyenesen maradnak). [1] Ez a tér dualitásának elve felé vezet. További általánosságok lehetségesek (lásd alább).
Ezek az elvek jó okot adnak arra, hogy a "szimmetrikus" kifejezést használják az előfordulási arányhoz. Így a mondat "a pont az egyenes vonal mentén" mondhatjuk, hogy "a pont és a vonal járulékos", és a nyilatkozat kettősítéséhez elegendő a "pont" szó, és a vonal helyeken átrendeződik ("a vonal és a pont járulékos").
Definíció szerint a projektív sík pontok és sorok halmaza, és a projektív átalakítás pontokat, pontokat és egyenes vonalakat mutat egyenes vonalakra. Az ilyen átalakulást kollandnak nevezik. [2] A projektív sík dualitásának vizsgálata során egy másik leképezést veszünk figyelembe, amelyben a pontok egyenesekké és egyenesekké alakulnak pontokká. Az ilyen leképezést korrelációnak nevezik. [3] A projektív leképezést a megőrzési követelmények határozzák meg
1) a kettős arány 2 pontjai és vonalak előfordulása [4]
Kettős tételek [| ]
Mivel az igazi projektív sík PG (2, R) önmagában kettős, számos jól ismert állítás kettős egymásra. Közülük:
A kettősség mint leképezés [| ]
A kettősség (sík) a C = (P, L, I) projektív síkból történő leképezése a kettős C * = (L, P, I *) számára, amely megőrzi az incidencia tulajdonságát. Így a kettősség (sík) σ olyan pontot képvisel az közvetlen és egyenes a pont (P σ = L és L σ = P), oly módon, hogy ha Q fekszik a vonalon m (jelöljük QI m), akkor Q σ I * m σ ⇔ m σ IQ σ. A dualitás (sík), amely egy izomorfizmus, korrelációnak nevezik. [5] A korreláció létezése a projektív sík önk dualitását jelenti.
Abban a különleges esetben, amikor a projektív sík PG (2, K) típusú, ahol K egy osztódógyűrű, a dualitást kölcsönös átalakulásnak nevezik. [6] A projektív geometria alapértelmezett tétele szerint a kölcsönös transzformáció egy automorfikus függvény összetétele a K és a projektív átalakításon. Ha az alkalmazott automorfizmus azonos, akkor a kölcsönös transzformációt projekciós korrelációnak nevezik.
A másodrendű (véletlen) összefüggést polaritásnak nevezzük. Ha a korreláció nem polaritás, akkor φ2 nem triviális kollanja.
A leképezés fogalmát kiterjeszthetjük a nagyobb dimenziókra is, így a síkra való hivatkozás eltávolítható.
A nagy dimenziók kettősége [| ]
A projektív sík kettősége a kettősség különleges esete a projektív terek számára. Konverziók PG (n, k) (amelyek jelöljük KP n), ahol K - mező, cseréje R dimenzió objektumokat a tárgyak a dimenzió n - 1 - R (= kodimenziós r + 1). Így egy projektív térben n dimenziós a pont (dimenzió 0) fog megfelelni hipersíkokat (kodimenziós 1), a vonalak áthaladó két pont (dimenzió 1) felel meg a kereszteződés két hipersíkokat (kodimenziós 2), és így tovább.
Point of PG (n, k) lehet tekinteni, mint egy nem-nulla vektor a (n + 1) dimenziós vektortér feletti K., amelyben azonosítjuk a két vektor, ha eltérnek csak skaláris szorzás. Az n-dimenziós projektív tér mindkét pontjának egy másik módja a Kn + 1 eredetén áthaladó vonalak. Ezek az 1-dimenziós vektor szubpaces. Így a Kn + 1 mező n-dimenziós vektor-szubszekvenciái a projektív n-terek (K) fölött lévő (n-1) -dimenziós geometriai hiperplánjait reprezentálják.
Egy nem nulla vektor a Kn + 1-ben egy (n-1) -dimenziós geometriai alterületet (hyperplane) definiál Hu,
Az u. amit a hyperplán meghatározására használunk, az UH-val jelöljük. és a vektor végéhez tartozó pontot jelöljük, az uP jelölést használjuk. A szokásos skaláris termék szempontjából. Hu = xP: uH • xP = 0>. Mivel K egy mező, a skalár termék szimmetrikus, ami azt jelenti, hogy uH • xP = u0 x0 + u1 x1 +. + un xn = x0 u0 + x1 u1 +. + xn un = xH • uP. Meg lehet határozni a kölcsönös transzformációt uP ↔ Hu a pontok és a hyperplanes között. Ez a levelezés kiterjeszthető a két pont által alkotott egyenesre és a két hiperplán metszéspontjára, és így tovább.
A projektív sík PG (2, K), amely a területen K van megfelelő: homogén koordináták (a, b, c) ↔ vonalak által adott egyenletek ax + by + cz = 0. A projektív térben PG (3, K) megfelelő külleme pont homogén koordinátákkal (a, b, c, d) ↔ sík által adott egyenletek ax + by + cz + DW = 0. Ez a levelezés is mutatja, a által meghatározott egyenes két pont (a1, b1, c1, d1) és (a2, B2, C2, D2), egy egyenes vonal, amely a két síkja egymást metszi egyenletek által meghatározott a1 x + b1 y + c1 z + d1 w = 0, és A2 x + b2 y + c2 z + d2 w = 0.
Háromdimenziós tér [| ]
A valódi projektív 3-dimenziós tér PG (3, R) poláris térképein a pontok megfelelnek a síkoknak, és a vonalak megfelelnek a vonalaknak. A sztereometriában kettős poliéder van. amikor a pontok kettősek az arcokhoz, és a szélek kettősek a széleknél, úgyhogy az icosahedron kettősdik egy dodekaéderhez. és a kocka kettős az oktaéderhez.
A kölcsönös átalakulás geometriai konstrukciója [| ]
A PG (2, R) homogén koordinátákban való megfelelést geometrikusan lehet leírni. Erre a célra az igazi modell projektív sík [en] „egység gömb azonosító antipodes [7]”, vagy azzal egyenértékű, a modell vonalak és síkok, az origón áthaladó, a koordinátarendszerben R 3. társítani a sor, az origón áthaladó, síkjára merőleges a talp, amely tartalmazza a származást. Ha ezt a modellt tartják egyenes pontok és a sík - egyenes projektív sík PG (2, R), ez az összehasonlítás válik levelezés (és tulajdonképpen - poláris mapping) A projektív sík. Gömb alakú mintát lehet elérni a koordináták eredetén áthaladó vonalak és síkok metszéspontjánál, egy olyan egységgömbnél, amelynek központja az eredetnek. A vonalak metszi a gömböt két ellentétes ponton, amelyek a projektív sík pontjának megszerzésére vannak azonosítva, és a síkok nagy körökön metszenek a gömbön. amelyek a projektív sík vonalai.
Az a tény, hogy egy ilyen összehasonlítás "megőrzi" az incidenciát, könnyen megmutatható az egyenes vonalak és repülőgépek modelljén. A projektív sík egyenes vonalához tartozó pont megfelel a modell síkjában fekvő egyenes vonalnak. Az összehasonlítás szerint a sík egyenes vonalat jelent, amely áthalad az eredeten és merőleges a síkra. Ez a kép (egyenes vonal) merőleges a síkon fekvő bármely egyenesre, és különösen az eredeti egyenes vonalra (a projektív sík pontjai). Az eredeti vonalra merőleges egyenes vonalak egy olyan síkot képeznek, amely az eredeti vonalhoz tartozó sík. Így a vonal képe a sík képében rejlik, így az incidencia megmarad.
Lengyelek és lengyelek [| ]
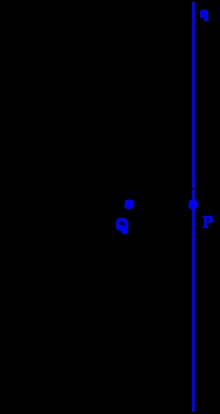
A pólus és a poláris az O. P = Q 'körhöz. q poláris a Q-re. Q egy q pole.
Euklideszi térben a C középpontot és az "O" középpontot és a r sugárzást rögzítjük. Az O ponttól eltérő pontoknál a Q 'képét definiáljuk. így az OP • OQ = r 2. A P → Q leképezés inverz [en] [8] a C körhöz képest. Az egyenes vonal q. A P. átmenő az OP-re merőlegesen. a Q pontnak a C körhöz viszonyított polárisja.
Legyen q egy olyan vonal, amely nem áthalad az O-on. A merőlegeset O-ről q-re csökkentjük. amely Q ponton keresztezi a pontot (ez az O vonal legközelebbi vonalának pontja). A Q ponttal (P pont) a C függvényében fordított inverziós képét a q vonal pole-jának nevezzük. Ha a pont fekszik egy egyenes vonal M Q (amely nem halad át O), a pólus vonal q fekszik a poláris M pont, és fordítva. Az incidenciát megőrző folyamatot, amelyben a pontok és a vonalak a C oszlopokhoz és oszlopokhoz kapcsolódnak, projektív átalakulásnak nevezik. [9]
Ahhoz, hogy ez a folyamat a kölcsönös átalakulás euklideszi térben (nem projektív sík) ki kell terjednie a kiterjesztett euklideszi síkban úgy, hogy a vonal a végtelenben [en] és pont a végtelenben [en]. amelyek ezen a végtelenül távoli vonalon fekszenek. Ez a kiterjesztett sík, definiáljuk a poláros O pont, mint egy vonal a végtelenben (és O a pole a végtelenben), és a pólusok egyenes vonalak áthaladó O végtelenben ponton, ahol, ha a vonal meredeksége s (≠ 0), a pólus egy végtelenül távoli pont, amely megfelel a -1 / s lejtésű párhuzamos vonalaknak. Pole az x-tengely - ez az a pont, végtelen függőleges vonalak és a pole y tengelyen - az a pont a végtelenben vízszintes vonalak.
Az invertálásnak a fenti körhöz viszonyított poláris transzformációjának konstrukciója a kúp alakú szakaszokon (a kiterjesztett valós síkon) inverzióval általánosítható. Az így kialakított kölcsönös átalakulás a második rend, azaz a poláris átalakulás projektív korrelációja.
A gömb térképezése a síkba [| ]
Az egysíkú gömbsugaras projektív sík modellje a planáris modell izomorf (figyelembe véve az előfordulási tulajdonságot), ahol a síkot a végtelenített projekciós vonallal meghosszabbítják. Ebben a modellben a gömb ellentétes pontjai (a központhoz viszonyítva) egy pontnak tekintendők.
Ha egy gömb pontját egy síkra hasonlítjuk, azt feltételezzük, hogy a gömb egy bizonyos ponton érintkezik a síkkal, és ezt a pontot a sík eredetének tekintjük. Most rajzoljon egy vonalat a gömb pontján és a gömb középpontján. Ez az egyenes egy bizonyos ponton áthalad a gömbön. Az így kapott pont használható egy-egy mapping készítéséhez
Egyenes vonalak egy gömb körmeinek nagy kiterjedései, mivel egy sík egy síkban egyenes vonal mentén húzható meg, és a háromdimenziós koordináták eredete, és ez a sík egy nagy kör mentén metszi a gömböt.
Amint látható, a gömbön lévő nagy kör egy projektív ponttal társítható, amely egy olyan egyenes vonalnak felel meg, amely merőleges a síkra, amelyen a kör fekszik, és amely kettősnek tekinthető. Ez az egyenes áthalad az érintő síkon, és ez azt mutatja, hogyan társítson egy sík egyetlen pontját a sík bármely vonalán, hogy a pont kettős legyen a vonalhoz.