14 Opció
14.1. Az ábrán a töltés q függése látható a t időben egy ideális oszcilláló áramkörben. A kondenzátor elektromos mezőjének energiájában fellépő oszcilláció időszaka
1) 2 μs 2) 4 μs 3) 6 μs 4) 8 μs
14.2. A pont harmonikus rezgéseket okoz. Az oszcillációs periódus T = 2 s, az oszcillációk amplitúdója A = 50 mm, a kezdeti fázis φ0 = 0. A pont sebességét a t időpontban kell keresni. Ha a pont elmozdulása az egyensúlyi helyzetből 25 mm.
14.3. Meg kell találni a vibrációs áramkör Wm mágneses mezőjének energiáját Wel (Wm / Wel) villamos mező energiájához a t = T / 8 időtartamra.
14.4. A amplitúdója a kapott oszcilláció, ami a kívül két egyformán irányított harmonikus rezgések azonos frekvencia, amelynek a fáziskülönbség 60 értéke 0. A = 6 cm. A kezdeti szakaszában az első oszcilláció nulla. Határozzuk meg a második oszcilláció A2 amplitúdóját, ha A1 = 5 cm. Vektordiagramot hozzunk létre az amplitúdók hozzáadásához.
14.5. Anyag pont részt egyidejűleg két kölcsönösen merőleges rezgéseket által kifejezett egyenletek x = sinωt 2 cm és y = -1 cos ωt cm. Find az egyenlet a pontjának pályája. Rajzoljunk egy vonalat a pont mozgására, és mutassuk meg a mozgás irányát.
14.6. Az oszcillációk csillapításának logaritmikus csökkenése az áramkörben λ = 0,003. Határozzuk meg az N összes oszcilláció számát, amely alatt a töltés amplitúdója a kondenzátor lemezén 2-szeresére csökkent.
14.7. Egy sík monokróm hullám propagál egy rugalmas közegben. A t = 0 kezdeti időpontjában a tápközeg összes részecske nyugalmi állapotban volt. Az ábrán az oszcilláció forrásától elválasztott részecske eltolódásának időfüggése látható x = 2 m távolsággal. Mi a hullámhossza (SI-ben)? Mi a különbség (SI-ben) a forrásból elválasztott közegben a részecskék oszcillációinak fáziskülönbségével x1 = 1 m és x2 = 3 m távolságban?
14.8. Egy hullám az oszcillációs forrásból egyenes vonal mentén terjed. Az oszcillációk amplitúdója A = 10 cm. Mi a távoli pont eltolódása a forrásból l = 0,75λ távolságban. amikor az oszcilláció kezdetétől eltelt idő t = 0,9 T?
14.9. A nyilak alatt jelzik az Umov-Poytinga lapos elektromágneses hullám sebesség vektorát és vektorát.
Milyen esetekben vannak a vektorok és hullámok a 0z síkokban. Adja meg az ábrák számának összegét.
14.10. A hossza az elektromágneses hullám vákuumban, amelyen a rezgőkör van konfigurálva, ha a maximális kondenzátor töltésének lemezeken Qm = 50 NC, és a maximális áram az áramkörben Im = 1,5 A. Az aktív hurok ellenállás elhanyagolható.
Oszcilláció és hullám-ingadozások
15 Opció
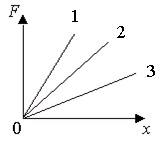
15.1. Egy anyagm tömegpont m harmonikus oszcillációt hajt végre. Az ábra az x elmozdulásra ható kvázi-rugalmas erő F modulusának függvényét mutatja. Melyik gráf megfelel a pont harmonikus oszcillációinak szögfrekvenciájának legnagyobb értékével?
15.2. A k különböző rugalmassági együtthatókkal és azonos tömegű m-es rendszerek harmonikus oszcillációival egyenleteket adunk meg. Melyik esetben a rugalmasság legkisebb együtthatója? Erősítse meg a választását számításokkal.
1) x = 2 cos (3 π t + π), cm 2) х = 3 cos (2 π t + π), cm
4) x = 3 cos (5π t + π / 2), cm 8) x = 4 cos (4 π t + π / 2)
15.3. Az oszcilláló áramkör egy L = 0,2 mH induktivitású tekercs és egy S = 155 cm 2 lemezes területű kondenzátorból áll. A távolságuk d = 1,5 mm. Tudva, hogy a kontúr egy λ = 630 m hullámhosszon rezonál, meghatározza a kondenzátor lemezei közötti tér kitöltésére szolgáló közeg dielektromos állandóját.
15.4. Két azonos irányú harmonikus oszcillációt ír le, amelyet az x1 = 3cm2 = 3cm egyenlet ír le. Határozzuk meg a kapott oszcilláció amplitúdóját és kezdeti fázisát, és írjuk le az eredményül kapott oszcilláció egyenletét. Adjon vektordiagramot az amplitúdók hozzáadásához.
15.5. A pont mozgását az x = A1 és y = A2 egyenletek adják meg. ahol A1 = 10 cm, A2 = 5 cm, ω = 2 s-1. τ = π / 4 s. Keresse meg a pont pályájának egyenletét. Rajzoljunk egy vonalat a pont mozgására, és mutassuk meg a mozgás irányát.
15.6. A tömeg tömege m = 1 kg bonyolult közegben, amelynek együtthatója r = 0,05 kg / s. Két azonos rugalmasságú k = 50 N / m rugó segítségével minden testet egyensúlyi helyzetben tartanak, a rugók nem deformálódnak. A testet elmozdítottuk az egyensúlyi helyzetből és felszabadítottuk. Határozzuk meg a csillapítási együtthatót és az oszcillációk számát, amelyek után az amplitúdó egy e tényezővel csökken.
15.7. Egy sík monokróm hullám propagál egy rugalmas közegben.
A nyilak alatt jelzik a közeg részecskéinek vibrációját.
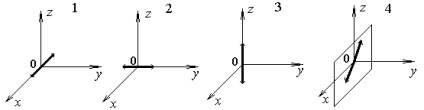
Milyen esetekben lehet a hullám sebesség vektor a 0y síkban feküdni. ha a hullám hosszirányú? Adja meg a megfelelő diagramok számát.
15.8. Egyenlet csillapítatlan oszcilláció rendelkezik formájában ξ = sin 2,5 πt cm. Find elmozdulás az egyensúlyi helyzet, sebesség és gyorsulás egy pont található a parttól L = 20 m-re a rezgésforrás, t = 1 s kezdete után oszcilláció. Az oszcillációk szaporítási sebessége v = 100 m / s.
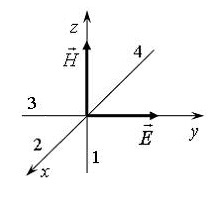
15.9 Az ábra az elektromágneses hullám elektromágneses () és mágneses () mezők vektorainak tájolását mutatja.
Az elektromágneses hullám fázis sebesség vektora ...
15.10. Az ábrán az elektromágneses hullám elektromos elemének pillanatnyi fényképe látható az 1 közegtől a 2 közegig, amely merőleges az AB médium határáig.
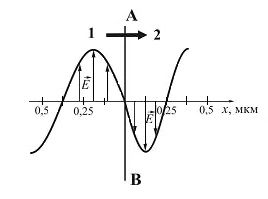
Határozzuk meg a fénysebesség arányát a 2 közegben az 1 közegben levő sebességhez viszonyítva.
Oszcilláció és hullám-ingadozások
16.1. Az ábrák egy harmonikus törvény szerint oszcilláló anyagpont koordinátájával és sebességével függnek össze.
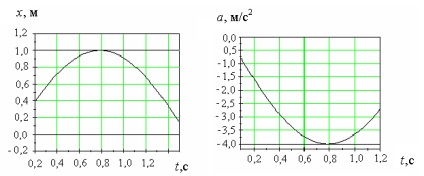
A pont oszcillációinak ciklikus frekvenciája ...
1) 2 s -1 2) 3 s -1 3) 1 s -1 4) 4 s -1
16.2. Olyan anyagi pont, amely ν = 1 Hz frekvenciájú harmonikus rezgéseket hajt végre, t = 0 időpontban x0 = 5 cm koordinátával, υ0 = 15 cm / s sebességgel. Határozza meg az oszcillációk amplitúdóját.
16.3. Az oszcillációs áramkörben fellépő szabad csendes oszcilláció energiája 0,2 mJ. Amikor a kondenzátor lemezei lassan egymástól távolodtak, az oszcillációs frekvencia n = 3-szorosára nőtt. Határozza meg az elektromos tér erőivel szembeni munkát.
16.4. Az azonos periódusú T = 4 s egyenlő irányú harmonikus oszcillációk fáziseltolódása és ugyanaz az A = 5 cm amplitúdó π / 4. Írja le a két oszcilláció hozzáadásából adódó mozgás egyenletét, ha az első oszcilláció kezdeti fázisa megegyezik a kormányrúddal. Készítsen egy vektordiagramot ezen oszcillációk hozzáadásával.
16.5. Point végez egyidejűleg két harmonikus rezgések azonos frekvenciájú, előforduló egy egymásra merőleges irányban, és kifejezte az egyenletekben: x = A cos, y = b cos, ahol A = 2 cm, H = 3 cm Find az egyenlet a pálya pontok és a kivitelezést megfelelően a skála .. Adja meg a pont mozgásának irányát és magyarázza meg a választ.
16.6. Határozzuk meg a csillapított oszcilláció T időtartamát, ha a rendszer természetes oszcillációinak T0 időtartama 1 s, és a logaritmikus csillapítás csökkenés λ = 0,628.
16.7. Egy sík monokróm hullám propagál egy rugalmas közegben. A nyilak alatt jelzik a közeg részecskéinek vibrációját.
Milyen esetekben lehet a hullám sebesség vektor a 0y síkban feküdni. ha a hullám keresztirányú? Adja meg a megfelelő diagramok számát, és magyarázza el a választ.
16.8. A keresztirányú hullám a rugalmas zsinór mentén v = 15 m / s sebességgel terjed. A T időszakban a zsinór 1,2 pont rezgések amplitúdója A = 2 cm. Határozzuk meg a hullámhossz λ, és φ a fázis a oszcilláció és elmozdulás a pont ξ, távközzel elválasztott rezgésforrásnak a parttól x = 45 m távolságra van a hullám forrás időpontban t = 4 a.
16.9. A koordinátatengely párhuzamos síkban elektromágneses hullám terjed, ha egy bizonyos ideig a ponton koordinátái (x, y, z) = intenzitás az elektromos tér (E, 0,0), és a mágneses indukció = (0,0, B)?
1) párhuzamos az X tengellyel párhuzamosan az Y tengellyel párhuzamosan
3) párhuzamos a Z tengellyel 4) ilyen hullám lehetetlen
16.10. Egy mágneses permeabilitással rendelkező tápközegben = 1 és egy permettivitás = 9 sík elektromágneses hullám terjed a 0y tengely pozitív irányában. Az elektromos és mágneses térerősség értékei E = 750 V / m, H = 2 A / m. Határozzuk meg az elektromágneses hullám térfogati energiasűrűségét (mikro-joule / köbméter).
Oszcilláció és hullám-ingadozások