Isoquanta és típusai, a blogu - blog gazdasága
A fogyasztói kereslet modellezésénél a fogyasztási cikkek különböző kombinációi ugyanazt a szintjét grafikusan mutatják közömbösségi görbe alkalmazásával.
A gazdasági-matematikai termelési modellekben minden technológia grafikusan ábrázolható egy ponttal, amelynek koordinátái a K és L erőforrások minimálisan szükséges költségeit tükrözik egy adott kimeneti térfogat előállításához. Az ilyen pontok halmaza egy egyenlő kimenet, vagy izokvantum. Így a termelési függvényt grafikonként egy izokváns család képviseli. Minél messzebb van az eredetétől az izokvantum, annál több produkciót tükröz. Az indifferencia görbétől eltérően minden egyes izokvantum kvantitatívan meghatározott kimeneti térfogatot jellemez. Az 1. ábrán. A 6.1. Ábrán három izokváns látható, amely megfelel a 200, 300 és 400 egység termelési volumenének.
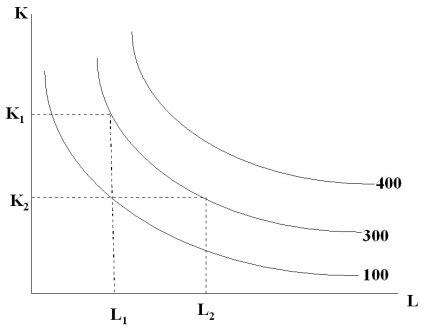
Ábra. 6.1. A különböző gyártási mennyiségeknek megfelelő izokvantumok
Azt mondhatjuk, hogy a termelés 300 egység szükséges tőke K1 és L1 egységek munkaerő egységek vagy K2 egységek a tőke vagy L2 egységek munkaerő, vagy bármely más kombinációja a sok, ami képviseli Y2 = 300 egyenlőtermék-görbe.
Általában az elfogadható termelési tényezőkészlet X sorában X megkülönböztethető egy, az előállítási funkció isoquantumának nevezett Xc részecske, amelyet az jellemez, hogy minden vektor esetében a következő egyenlőség áll:
Így az izokvantumnak megfelelő összes erőforráscsoport esetében az előállított termékek mennyisége egyenlő. Lényegében az izokvantum leírja a tényezők kölcsönös cseréjének lehetőségét a termelési folyamatban, ami változatlan termelési volument biztosít. Ebben a tekintetben meg lehet határozni az erőforrások kölcsönös cseréjének együtthatóját, bármely differenciális arány mellett bármely izokvantum mentén
.
Ezért a j és k faktor párhuzamos helyettesítésének együtthatója egyenlő:
.
Az így kapott arány azt mutatja, hogy ha a termelési erőforrásokat a növekményes termelékenység arányával megegyező mértékben kicserélik, akkor a kibocsátás mennyisége változatlan marad. Meg kell mondani, hogy a termelési funkció ismerete lehetővé teszi számunkra, hogy jellemezzük az erőforrások kölcsönös cseréjét a hatékony technológiai módszerek között. E cél elérése érdekében a termékek erőforrás-pótlási rugalmassági együtthatója:
,
amelyet az izokvantum mentén más termelési tényezők állandó költségszintje alapján számítanak ki. Az σjk értéke az erőforrások kölcsönös cseréjének együtthatója viszonylagos változásával jellemezhető, a köztük lévő kapcsolat változásával. Ha a cserélhető erőforrások aránya σjk százalékkal változik, akkor a kölcsönös cserearány 1 százalékkal változik. Egy lineáris termelési függvény esetében a kölcsönös cserearány változatlan marad a használt erőforrások bármely arányával, ezért feltételezhető, hogy a rugalmasság. Ennek megfelelően az σjk nagy értékei azt mutatják, hogy nagy a szabadság a termelési tényezők helyett az izokvantum mentén, és a termelési funkció fő jellemzői (termelékenység, átváltási arány) nagyon kevéssé változnak.
Minden felcserélhető erőforráshoz tartozó energiatermelési funkciók esetén az egyenlőség σjk = 1 érvényes. Az előrejelzés és az előrendezési számítások gyakorlatában gyakran használják a helyettesítés állandó rugalmasságának (CES) funkcióit, amelynek formája:
.
Erre a funkcióra az erőforrás rugalmassági rugalmassági együttható:
és nem változik az elköltött erőforrások mennyiségétől és arányától függően. Az σjk kisebb értékeinél az erőforrások csak kis méretben helyettesíthetik egymást, és a σjk = 0 határában elvesztik a felcserélhetőségi tulajdonságokat, és csak a konstans arányban jelennek meg a gyártási folyamatban, azaz kiegészítik egymást. A kiegészítő erőforrások használatának termelését leíró termelési függvény egy példája a "kimeneti költség" funkció, amely így néz ki:
,
ahol aj a j. termelési tényező erőforrás-visszanyerésének állandó együtthatója. Nem nehéz meglátni, hogy egy ilyen termelési függvény meghatározza a "szűk keresztmetszet" felszabadulását az alkalmazott termelési tényezőkön. A kinyerési rugalmassági együtthatók különböző értékeire vonatkozó termelési függvények különböző viselkedési eseteit a grafikon mutatja (6.2. Ábra).
Egy effektív technológiai készlet ábrázolása a skaláris termelési függvény segítségével elégtelennek bizonyul azokban az esetekben, amikor egy ipari létesítmény teljesítményét leíró egyetlen mutatóval lehetetlen, de több (M) kimeneti mutatót kell használni. Ilyen körülmények között használhatjuk a vektor termelési függvényt:
,
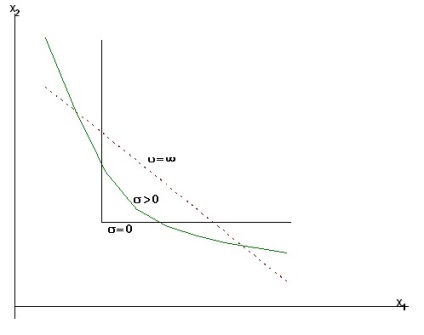
Ábra. 6.2. Az izokvant viselkedés különböző esetei
A marginális (differenciált) termelékenység fontos fogalmát a reláció vezette be:
,
Hasonló generalizáció elismeri a skaláris FS többi fő jellemzőjét.
Az indifferencia görbékhez hasonlóan az izokvantumok is különböző típusúak.
Az űrlap lineáris termelési függvényében:
Y = A + b1K + b2L, ahol
Y - termelési mennyiség;
A, b1, b2 paraméterek;
K, L - a tőke költsége és ott,
és egy erőforrás egy másik izokvantum általi teljes cseréje lineáris alakú lesz (6.3. ábra).
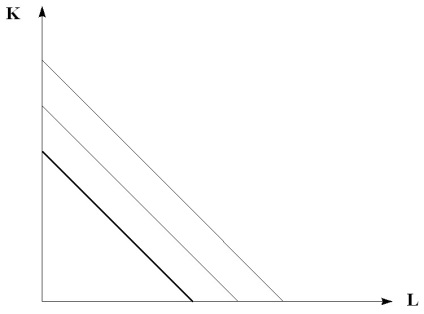
Ábra. 6.3. Lineáris típusú izokvánsok
Az Y = AKαLβ energiatermelési funkcióhoz görbék formájában (6.4. Ábra).
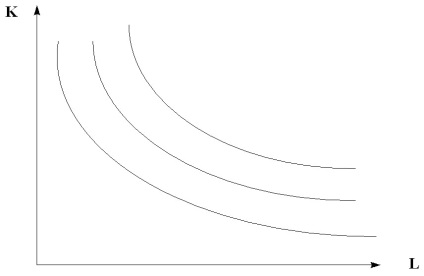
Ábra. 6.4. Az energiatermelési funkció izokvantjai
Ha az izokvantum csak egy technológiai módszert tükröz e termék előállítása során, akkor a munka és a tőke az egyetlen lehetséges kombinációban áll össze (6.5.
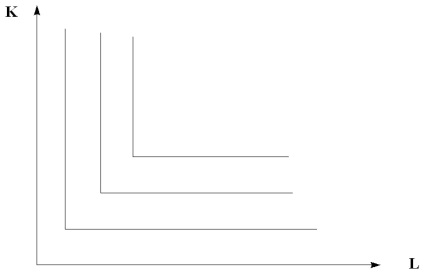
Ábra. 6.5. Ikvasok merev kiegészítő erőforrásokkal
Ezek néha a egyenlőtermék-görbe egyenlőtermék-görbe Leontief típusát, miután az amerikai közgazdász Leontief, aki ezt a fajta isoquants alapján a módszer a bemenet-kimenet (Input - Output).
Az ilyen konfigurációjú izokvantákat lineáris programozásban használják az optimális erőforráselosztás elméletének igazolására. A törött izokvantumok leginkább reálisan reprezentálják számos gyártó létesítmény technológiai képességét. Azonban a gazdasági elméletben hagyományosan használják az izokvant-görbéket, amelyek a növekvő számú technológiával rendelkező poligonális vonalakból és a törési pontok növekedéséből származnak.