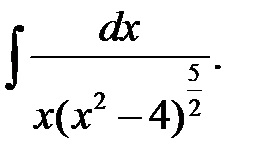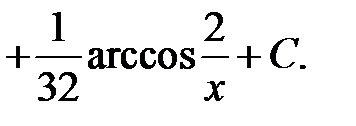Frakcionális-lineáris szubsztitúció

1). Ha az integrand gyökerei formában vannak, stb. ahol n, m, q, p, s, r stb. természetes számok, akkor szubsztitúcióval racionális frakcióvá alakul. ahol k a gyökér exponensek legkisebb közös többszörösének u.

2). Ha az integrand gyökerei formában vannak, stb. n, m, q, p, s, r stb. természetes számok, akkor szubsztitúcióval racionális frakcióvá alakul. ahol k a gyökér exponensek legkisebb közös többszöröse és

.

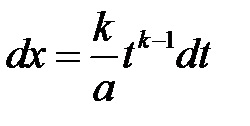
3). Ha az integrand gyökerei a formában vannak

. ahol n természetes szám, akkor helyettesítést alkalmazunk . ahol

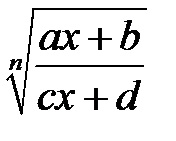
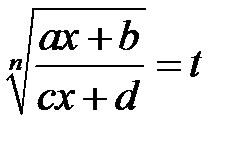
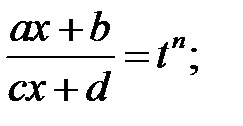
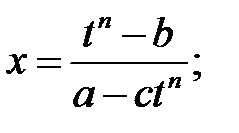
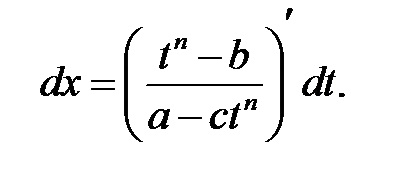
PÉLDA Keresse meg az integrálokat: a)

b) ;

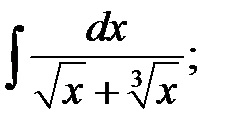
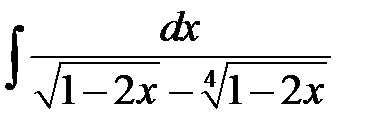
Megjegyzés: A integrandban az x második és harmadik hatványának gyökerei vannak, ezért a helyettesítés x = t 6. ahol a 6 a legkisebb közös szám két és harmadik számmal.

7.2. Az irracionalitások trigonometrikus permutációval történő integrálása. A faj integrálódása a teljes négyzet radikális jele szerinti kiválasztás után és a lineáris szubsztitúció alkalmazása

a következő három típus valamelyikét integráljuk: A megfelelő trigonometriai szubsztitúció használatával e három típus integrálja egy funkció integrálására, amely racionálisan függ a sin x és cos x függvényektől.

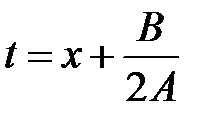
1. az űrlap integrálva; helyettesítés

Példa: Határozatlan integrál keresés.

R eshenie: Hogy megszabaduljunk a radikustól, helyettesítünk és helyettesítjük a végtelen integrálist

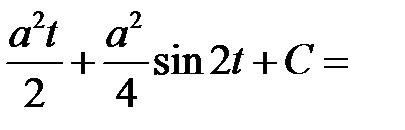
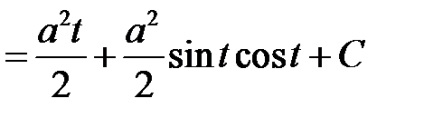
2. az űrlap integrálva;

PÉLDA: Határozza meg a meghatározatlan integrált elemet

.

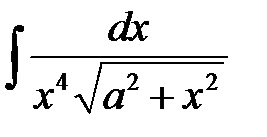
Megoldás A helyettesítés segítségével az irracionális funkció integrálját a bűnre nézve ésszerűvé tesszük.

=

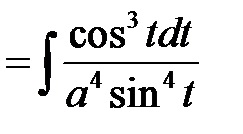
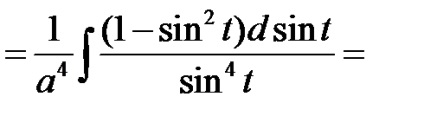
3. az űrlap integrálva;

PÉLDA: Határozza meg a meghatározatlan integrált elemet