Wolframalpha orosz folyamatos valószínűségi eloszlások a wolframban, alfa
Folyamatos valószínűségeloszlások Wolframban | Alpha
A valószínűségi eloszlások kivételesen fontos szerepet játszanak a matematikában, a statisztikában, a matematikai modellezésben, a fizikában stb. Ebben a témában a Wolfram | Alpha mindig is siet, hogy segítsen nekünk. Például ha hirtelen szükség lenne egy információval a valószínűségi eloszlás tulajdonságaira (a folyamatos eloszlás tulajdonságai), akkor a megfelelő lekérdezéssel forduljon a Wolfram | Alpha-hoz, és azonnal megkapja a szükséges információkat. A legfontosabb az, hogy helyesen tegye fel a kérdést a Wolfram | Alpha-nak, vagyis helyesen fogalmazza meg a szükséges lekérdezést.
Ebben a megjegyzésben megtalálja a választ arra a kérdésre, hogyan kell használni a Wolfram | Alpha-t, hogy válaszokat kapjunk a folyamatos véletlen változók fő probabilisztikus eloszlásának tulajdonságaira vonatkozóan.
A legtöbb esetben, annak érdekében, hogy a valószínűségi eloszlásokra vonatkozó információkért a Wolfram | Alpha-ra megfelelően hivatkozzunk, emlékeznünk kell arra, hogy a valószínűségi eloszlás nevét angol nyelven írjuk le. Ez mindenekelőtt az ismert normál eloszlásokra vonatkozik, amelyeket szintén Gauss eloszlásnak neveznek.
Alapvető információk a normál eloszlásról, nevezetesen tulajdonságairól, grafikonjairól, numerikus jellemzőiről - A Wolfram | Alpha megjeleníti a normál eloszlás (gauss eloszlás) kérésre:
Először is a lekérdezéshez a normál eloszlás alapelosztási jellemzőire (normál eloszlású statisztikai tulajdonságokra) vonatkozó listát kapsz:
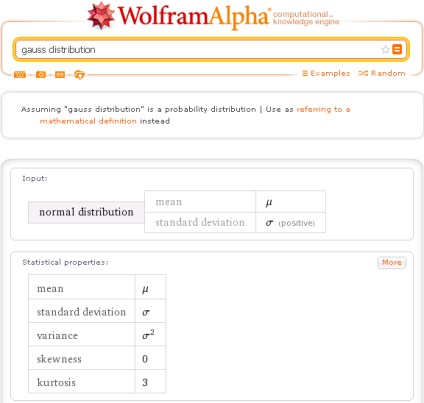
- Átlag - átlag, átlag;
- Standard eltérés - az átlag-négyzet eltérés;
- Variancia - variancia;
- Hajlékonyság - aszimmetria;
- A kurtózis túlzás.
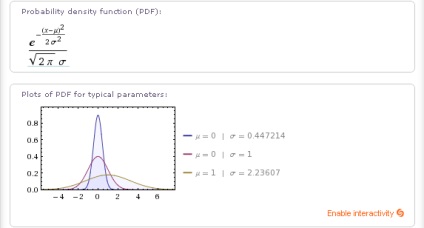
Szintén - a kumulatív eloszlásfüggvény (CDF) képlet és grafikonja:
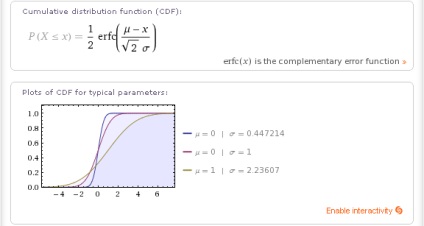
Végül, harmadszor, a Wolfram | Alpha a normál eloszlás néhány fontos százalékát mutatja:
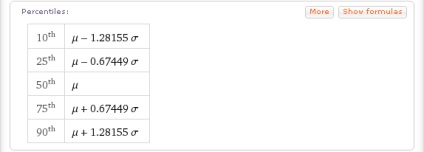
Hasonlóképpen ugyanazt az alapinformációt is megkaphatjuk a többi folytonos valószínűségi eloszlásról. Az alábbiakban felsoroljuk a legfontosabbakat a megfelelő kérésekkel:
Ha a folyamatos valószínűségi eloszlások különálló tulajdonságait kell beszerezni, akkor a lekérdezésben az elosztási név előtt egyszerűen adja meg a szükséges tulajdonságot. Például, ha normál eloszlásra számíthatsz, akkor az átlagos rendes elosztási lekérdezést kell használnod. A normál eloszlás sűrűségének eléréséhez használja a pdf normál eloszlási lekérdezést. A normál elosztási lekérdezés a normál eloszlásfüggvényt mutatja, és így tovább. Legyen óvatos - lekérdezésekor használja az angol billentyűzetkiosztást.
A következő bejegyzésben fogok mutatni részletesebben, segítségével néhány lekérdezést, akkor kap néhány tulajdonságát valószínűségi eloszlás, hogyan lehet a tulajdonságait valószínűségi eloszlásra az adott paraméterek mellett, a lista a főbb Diszkrét valószínűségi, valamint megmutatja, hogyan kell használni Wolfram | Alpha kiszámítja a valószínűsége, hogy egy véletlenszerűen változó hit egy adott intervallumban. By the way, az utolsó probléma a Wolfram | Alpha segítségével egyenlõen megoldható minden disztribúcióra. Ez azért fontos tudni, mert az egyetemi oktatásban (különösen a nem-matematikai karok egyetemek), ezt a problémát kezelni, általában szintjén a példa, és akkor is csak a normális eloszlás folytonos valószínűségi változók, valamint a binomiális eloszlás diszkrét valószínűségi változók.