A létesítmény leírása
Laboratóriumi munka №3
AZ OBERBURG OVERBELLA INERTIA MOMENTUM MEGHATÁROZÁSA
Határozzuk meg kísérletesen az inga tehetetlenségi nyomatékát, figyelembe véve az ellenállási erők fékezési nyomatékának hatását.
Az inga tehetetlenségi nyomatékának kísérleti függőségeinek vizsgálata az inga rudakra rögzített terheknek a forgástengelyre rögzített távolsága és összehasonlítása az elméleti függőséggel.
Számítsuk ki az Oberbeck inga tehetetlenségi nyomatékát az inga csigában felcsavart menetes terhelés transzlációs mozgásának dinamikájával és az inga forgási mozgásának egyenletével.
A létesítmény leírása
Az Oberbeck inga egy kereszt, amely négy rúdból áll, amelyekhez hozzájuk kapcsolódik a tengelyhez csatlakozó dob (3.1 ábra). A rudakon ugyanolyan rakományt helyeznek el, amely a forgástengelytől távolabb rögzíthető. A dobon két különböző átmérőjű tárcsa van. Egy csavarral felcsavarodik a csigahenger, amelynek szabad vége egy súlyt rögzít. A terhelés hatására a fonal leereszkedik, és az ingát egy forgó mozgásra vezeti, amely feltehetőleg felgyorsul. A terhelés mozgásának időtartamát egy elektronikus stopperórával mérik, amelyet a "Start" gomb aktivál, és a leállást a fényérzékelő jele jelzi. A rakományt x távolsággal leeresztik. mért függőlegesen rögzített vonalzó. A berendezés egy elektromechanikus fékberendezéssel rendelkezik, amelynek vezérlése a fényérzékelő jelén történik.
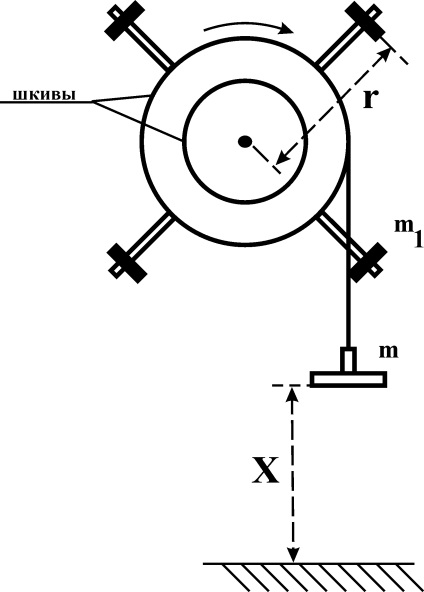
Az Oberbeck ingájának tehetetlenségi nyomatéka és az ellenállási erők pillanatának kiszámítása
Az inga-mechanikai rendszer mozgásának kiszámításához a transzlációs mozgás dinamikájának egyenletét alkalmazzuk egy menetre rögzített terhelés esetén, és az inga mozgás dinamikájának egyenletét.
A tömeg tömege gyorsulást eredményez az eredő gravitációs erő hatására és a menet feszességével (3.2 ábra). Írjuk le a Newton második törvényét a rakományra a mozgás irányába mutató vetületben:
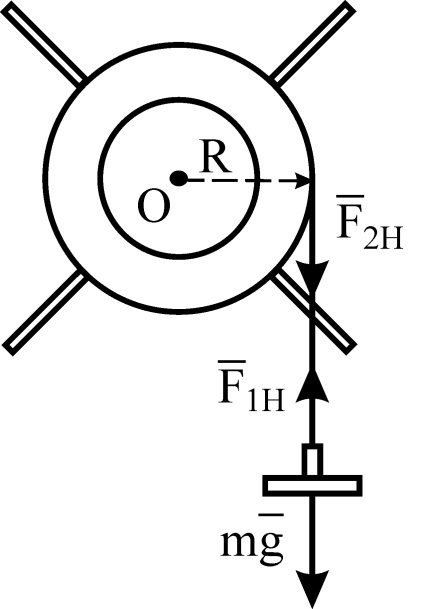
A feszítőerő átkerül a terhelésről a forgó inga csigájára. Ha feltételezzük, hogy a szál súlytalan, akkor a csigákon ható erő nagyságrenddel egyenlő és ellentétes irányban (Newton harmadik törvényének következménye). A feszítőerő egy forgási pillanatot hoz létre az "O" vízszintes tengelyhez képest. Ez a "mi tőlünk" tengely mentén irányul és az Oberbeck ingát hajtja. Ennek a pillanatnak a nagysága megegyezik azzal, hogy hol van a csavarmenet sugara, amelyen a csavarmenet fel van csavarva, hol van a csiga átmérője.
Az ellenállási erőnek a forgástengelyhez viszonyított pillanata az ellenkező irányba (felé) irányul.
Tegyük fel az inga számára a rotációs mozgás dinamikájának alapvető jogát:
hol van az erők élete,
- az inga tehetetlenségi nyomatéka,
Skálális formában ez az egyenlet van kialakítva (az erőcsavarok vektorainak vetületei és az O forgástengelyre merőleges gyorsulási várakozások rögzítése, amelynek irányát "tőlünk" választjuk):
A lineáris és a szögletes gyorsulás kinematikai viszonyának, valamint a nullázási sebesség nulla sebességének egyenletével a mért mennyiségeken keresztül expresszálhatjuk:
Megoldjuk a (3.1) és a (3.2) egyenletrendszert, amelyre szaporodunk (3.1) és hozzáadjuk (3.2):
Hangsúlyozzuk az Oberbeck ingájának tehetetlenségi nyomatékát:
Minden mennyiség, kivéve az egyenletben szereplőket, ismert. A kísérleti elhatározás problémáját vetjük fel.
Hadd legyenek az Oberbeck inga tehetetlenségi nyomatéka nélkül. A (3.4) bekezdésből következik
A kísérleti körülmények között, amely lehetővé teszi számunkra, hogy az (m) függését lineárisnak tekintsük.
Ez a függőség használható a mennyiség kísérleti becsléséhez. Valójában, ha a kísérletileg kapott függőséget extrapoláljuk az abszcissza tengelyre való metszésponttal, azaz azon a ponton, amelyen az egyenlőség teljesül (lásd 3.5), ez lehetővé teszi számunkra, hogy meghatározzuk, hogyan
Az inga tehetetlenségi nyomatékának meghatározásához (3.4) használjuk, ahol a mennyiséget előzetesen meghatároztuk az (m) és a (3.6) képlet alapján. A (3.3) és a (3.6) kifejezés (3.4) kifejezéssel való helyettesítésével megkapjuk a képletet az inga tehetetlenségi nyomatékának meghatározásához
A munkában használt Oberbeck-inga esetén az egyenlőtlenség érvényes. Figyelembe véve ezt:
A számításokhoz célszerű a tehetetlenségi nyomatékot a következő formában ábrázolni:
Az inga tehetetlenségi nyomatékának meghatározásához meg kell mérni a súlyt a távolság csökkentésével.
Az inga tehetetlenségi nyomatékának függése a terhelés távolságától a forgástengelyig
Az Oberbeck inga tehetetlenségi nyomatékát a dob hüvelyének a rudakkal () és a négy rakter tömegének tehetetlenségi nyomatékaival lehet ábrázolni, a r forgási tengely távolságaival rögzítve (). Ha ezeknek a súlyoknak a mérete kicsi, akkor lényeges pontnak tekinthetők. Anyagpont esetében a tehetetlenségi nyomaték egyenlő. Aztán az inga tehetetlenségi nyomatéka
Ez a függőség a tehetetlenségi nyomatéka terhelések távolság a forgástengely állítólag ellenőrizze, felhasználásával nyert eredmények általános képletű (3,7).
Az érték a kísérleti adatokból kiválasztható az Oberbek-inga tehetetlenségi nyomatékának meghatározása nélkül, feltételezve, hogy az ellenállási erők pillanata állandó marad.
Hozzárendelés a munkához
Miután elkezdett dolgozni, távolítsa el a rakományokat a rudakról, ha ott vannak.
Előzetesen válasszon egy jelet (például 50 cm), ahonnan a terhelés mozgása megkezdődik.
Az inga forgatásával a kezével fordítsa el a szálat egy nagyobb átmérőjű tárcsán, ügyelve arra, hogy a terhelés eléri a kiválasztott pozíciót.
Kapcsolja be az elektronikus stopperórát.
Végezze el az első élményt, terhelésként, egy szál húzásával, csak egy állvánnyal, tömeg nélkül terhelés nélkül. Mielőtt megnyomja a "Mode" gombot, állítsa a módot No.1-re (az "Mode 1" jelző világít). Ezután kattintson a "Start" gombra. Ez kikapcsolja az inga fékét, és a stopper egyszerre bekapcsol. Amikor az 1. üzemmód be van kapcsolva, a stopper automatikusan leáll, amikor a terhelés elhalad a terhelésen és a fékberendezés egyidejűleg működik. Adja meg az első kísérlet eredményeit a mérési táblázatban.
Töltsön el egy élményt, helyezze az állványra az elsőt, majd csak két terhelést. Adja hozzá az eredményeket a mérési táblázathoz. A (3.3) képlet segítségével számítsa ki a megfelelő értékek szögsebességének nagyságát.
Hozza létre a függőséget (m). Határozza meg az m0 értékét a gráfból az abszcissza tengelye metszéspontján. amelyhez = 0. Számítsuk ki az ellenállás erőinek pillanatnyi nagyságát (3.6).
Végezzünk öt egyenes mérést az adott távolság x terhelésének csökkentésére.
Számítsuk ki a t átlagos időtartamot és határozzuk meg a megbízhatósági hibát a P = 90%, n = 5 konfidencia valószínűséggel (lásd "Bevezetés").
A (3.7) képlet segítségével számoljuk ki a dob inerciáinak pillanatát a rudakkal.
Határozza meg a tehetetlenségi nyomaték közvetett mérésének bizonytalanságát (lásd "Bevezetés"), és rögzítse az eredményeket a formában.
Miután rögzítette az m1 terheléseket az inga rudakra a forgás tengelyénél egyenlő távolságra r, határozza meg ezt a távolságot a rudakra alkalmazott osztások és a telepítésre vonatkozó kezdeti adatok alapján.
Végezze el az egyszeri méréseket a terhelés csökkentésének tömegével m (válasszon egy értéket) egy csepp magasságra három különböző távolságban r a forgástengelytől.
Számítsd ki az inga tehetetlenségi nyomatékait a rudakra a (3.7) képlet szerint, különböző távolságokra r. Ebben az esetben, mint az előzetes kísérletek azt mutatják, lehetséges a megengedett pontossággal az m0 értékével használni a korábban a keresztre talált értékét a küllőkön lévő áruk nélkül. Hasonlítsuk össze a kapott adatokat a tehetetlenségi nyomaték értékével, a (3.8) képlet alapján számítva az r megfelelő értékekhez. Adja hozzá a számítás eredményeit a mérési táblázathoz.
Egyetlen rajzon rajzolja fel az inga tehetetlenségi nyomatékának kísérletileg kapott és elméletileg várható függőségének grafikonjait. Adja meg az egyes feladatok elvégzésével kapott eredményeknek megfelelő grafikonpontokat. Elemezze a lehetséges eltérések okait.
Tesztes kérdések
Mi a célja ennek a munkának?
A tehetetlenség pillanata, fizikai jelentése.
Hogyan változtathatom meg az Oberbeck inga tehetetlenségének pillanatát?
A transzlációs és forgó mozgás dinamikáinak egyenleteiből kiindulva a (3) általános képletből származik.
Ebben az esetben az inga mozgása egységesen felgyorsult?
Hogyan mérhető a távolság a forgástengelytől a rudakra rögzített súlypontokig?
Hogyan erősíti meg ez a munka a tehetetlenségi nyomaték lineáris függősége a testek távolságának négyzetével a forgástengelyre?
Egyedi feladatok a laboratóriumi munkát végző csapattagok számára
A dandártulajdonos számát