Hogyan lehet megoldani a számítógépes tudomány 2. feladatát?
A műveletek sorrendje:
- ha a kifejezésben nincsenek zárójelek, először minden "NOT" műveletet végrehajtunk, majd - "ÉS", majd - "VAGY", következtetés, ekvivalencia
Bővebben a logikai műveletekről:
- a logikai termék X ∙ Y ∙ Z ∙ ... egyenlő 1-gyel. a kifejezés csak akkor igaz, ha minden tényező egyenlő 1-gyel (és egyébként egyenlő 0-val)
- az X + Y + Z + logikai összeg egyenlő 0-val. a kifejezés csak akkor hamis, ha az összes kifejezés 0 (és más esetekben 1)
Feladat megoldása 2 USE a számítástechnikában
Az F logikai függvényt a (y → x) ∧ (y → z) ∧ z kifejezés adja. Határozzuk meg, hogy az F igazságtáblájának mely oszlopa felel meg az x változóknak. y. z.
Írja be a válaszba az x betűket. y. z a megfelelő oszlopok sorrendjében.
- Alapvetően logikus műveletet kell végezni, amelyet az utolsó fordulóban végezzünk el - logikus AND (összefogás) vagy ∧
- A kapcsolódás könnyebb megnézni az asztal azon sorait, ahol az F = 1 függvény
- Mivel a funkció az összefüggésben csak akkor igaz, ha az összes változó igaz, akkor szükség van, hogy külön minden egyes kapocs igaz volt ((y → x) = 1, és (y → z) = 1), és a változó Z is igaz volt (1)
- Mivel nehezebben zárójelekkel dolgozni, először meg kell határoznunk, hogy melyik oszlopnak felel meg. Ehhez kiválasztunk egy sort, ahol F = 1, és a fennmaradó cellákban csak egy egység, és a fennmaradó nullák:
- Mivel mindegyik kifejezésben 5 változó van, ezek az 5 változók 32 sorból álló igazságtáblát generálnak: mindegyik változó két értékből (0 vagy 1) veheti fel, akkor az öt változóval rendelkező különböző változatok 2 5 = 32. azaz 32 sor.
- Ebből a 32 sorból minden kifejezés (és F és G) biztosan tudjuk, hogy mindössze 5 sor: 4 közülük 1, és egy 0.
- A kérdés az F ∨ G kifejezés igazságtáblájára vonatkozó sorok számának = 1. Ez a kifejezés egy olyan diszjunkció, amely csak egy esetben hibás - ha F = 0 és egyidejűleg G = 0
- Az eredeti táblázatokban minden F és G kifejezésnél tudunk csak egy 0 létezéséről, azaz a fennmaradó sorokban lehet 1. Így. minden egyes kifejezésnél és F és G a 31 vonalon lehet egy (32-1 = 31), és csak egy nulla.
- Akkor az F ∨ G kifejezés csak egy esetben lesz 0, ha mind F = 0, mind G = 0:
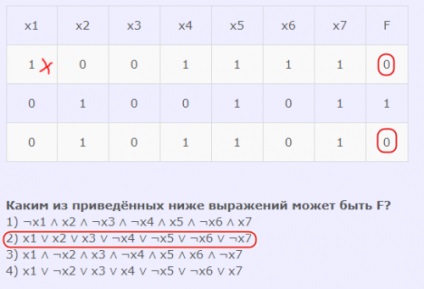
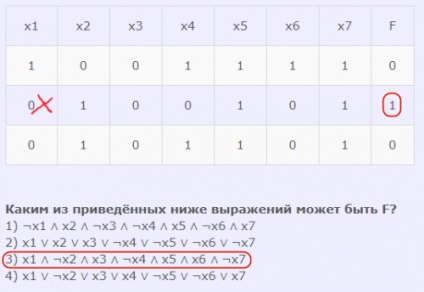
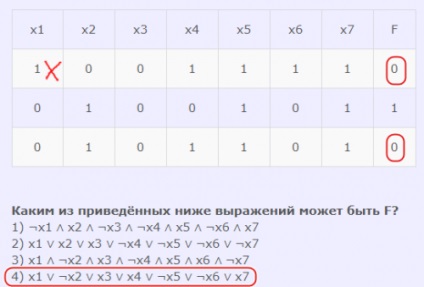
Az alábbi kifejezések közül melyik lehet F?
1) ¬x1 ∧ x2 ∧ ¬x3 ∧ ¬x4 ∧ x5 ∧ ¬x6 ∧ x7
2) x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ ¬x6 ∨ ¬x7
3) x1 ∧ ¬x2 ∧ x3 ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7
4) x1 ∨ ¬x2 ∨ x3 ∨ x4 ∨ ¬x5 ∨ ¬x6 ∨ x7
- Az első kifejezésben a fő művelet összefüggés. Ennek megfelelõen a második sorban a kifejezést ellenõrizzük, ahol a függvény = 1. Ha ebben a sorban a kifejezés minden argumentumát helyettesítjük, akkor a függvény visszatér a valóságba. Ie ez a kifejezés megfelelő.

A számítógépes ismeretekkel foglalkozó USE-feladat 2. határozata (K. Polyakov, 76. verzió):
Az "F" kifejezés igazságtáblázat-fragmense:
Adja meg ennek a kifejezésnek a teljes igazságtáblájának különböző sorainak lehetséges maximális számát, amelyben az x3 értéke nem egyezik meg F.
- A teljes igazságtáblának 2 6 = 64 vonala lesz (mivel 6 változó van).
- 4 sor ismeretes minket: ezekben az x3 nem egyezik kétszeresével.
- Ismeretlen sorok:
- Ismeretlen sztringekben az x3 nem egyezik meg az F-rel. Továbbá, két ismert vonalban az x3 nem egyezik meg F. Ennek megfelelően a nem megfelelő x3 és F sorok maximális száma lehetséges:
A számítógépes ismeretekkel foglalkozó USE-feladat 2. szakasza (K. Polyakov, 89. változat):
Minden A és B logikai kifejezés ugyanazon a 7 változótól függ. Ezeknek a kifejezéseknek az igazság tábláiban pontosan 4 egység van az érték oszlopban. Mekkora a maximálisan lehetséges egységek száma az A ∨ B igazság táblázat-értékeinek oszlopában?
- Az A és B kifejezések mindegyikének teljes igazságtáblája 2 7 = 128 sorból áll.
- Négy sorban a kifejezés eredménye egy, így a többi sorban - 0.
- A ∨ B igaz, ha A = 1 vagy B = 1. vagy mind A, mind B = 1.
- Mivel az A = 1 csak 4 esetben kapjuk meg azokat az eredményeket, amelyek visszaadják az igazságot az A ∨ B-nek (ahol B lehet 0 vagy 1):
A számítógépes tudomány (USE) feladatának 2. szakasza (K. Polyakov, 91. változat):
Minden logikai A és B kifejezés 8 változótól ugyanazon a halmazon múlik. Az egyes kifejezések igazságtábláiban az értékek oszlopa pontosan 6 egységet tartalmaz. Mekkora a nullák maximális száma az A ∧ B kifejezés igazság táblázat-értékeinek oszlopában?
- Az A és B kifejezések mindegyikének teljes igazságtáblája 2 8 = 256 sorból áll.
- 6 sorban a kifejezés eredménye egyenlő egy, majd a fennmaradó sorokban - 0.
- A ∧ B hibás abban az esetben, ha A = 0 vagy B = 0. Mindkét A és B = 0.
- Minden olyan esetben, ahol A = 1 lehet B = 0. majd az eredmény F = 0. Mivel meg kell találnunk a nullák maximális számát, akkor mindegyik hat A = 1 esetén B = 0-t társítunk. és fordítva, minden hat lehetséges B = 1 esetén A = 0
A számítógépes tudomány (USE) feladatának 2. Határozata (K. Polyakov, 58. verzió):
Logikai kifejezés alapján, 5 logikai változótól függően:
(¬x1 ∨ ¬x2 ∨ ¬x3 ∨ x4 ∨ x5) ∧ (x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5)
Hány különböző változóérték-készlet áll fenn, amelyre a kifejezés igaz?
- Mivel a kifejezés 5 változót tartalmaz, az igazságtábla 2 5 = 32 sorból áll
- Az alapművelet egy összefüggés (logikai szorzás), és a zárójelben egy diszjunkció (logikai kiegészítés)
- Jelöljük az első zárójelet az A-val és a második B-ra. Megkapjuk az A ∧ B kifejezést.
- Nézzük meg, hogy hány nullát találunk a kifejezés igazatáblájához:
Most vegye figyelembe minden esetben külön-külön:
Az USE informatikai feladatának (K.Polyakov 112-es változata) 2. határozata:
Az "F" kifejezés igazságtáblázat-fragmense:
Milyen kifejezés lehet F?
1) x1 ∧ (x2 → x3) ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7
2) x1 ∨ (¬x2 → x3) ∨ ¬x4 ∨ ¬x5 ∨ x6 ∨ ¬x7
3) ¬x1 ∧ (x2 → ¬x3) ∧ x4 ∧ ¬x5 ∧ x6 ∧ x7
4) ¬x1 ∨ (x2 → ¬x3) ∨ x4 ∨ x5 ∨ x6 ∧ x7
- Vegye figyelembe az egyes kifejezéseket külön-külön, és keresse meg az utolsó műveletet, amelyet végre kell hajtani.
Az F logikai függvényt kifejezéssel adjuk meg
¬a ∧ b ∧ (c ∨ ¬d)
Az alábbiakban az F. függvény igazságtáblájának töredéke található, amely tartalmazza az összes argumentumkészletet, amelyekre az F függvény igaz.
Határozzuk meg, hogy az F igazságtáblájának mely oszlopa felel meg az egyes változóknak. b. c. d.