Csillapított és kényszerített oszcilláció
Vibrációjának csillapítására úgynevezett rezgési amplitúdójának csökkenése az idő miatt a veszteséget a rezgési energia a rendszer (például, konvertáló rezgési energia hővé a súrlódás által mechanikai rendszerek). A csillapítás sérti az oszcillációk gyakoriságát, mivel ezek többé nem egy periodikus folyamat. Ha a csillapítás kicsi, akkor feltételesen használhatjuk az oszcillációs periódus fogalmát - T (a 7.6. Ábrán A0 az oszcillációk kezdeti amplitúdója).
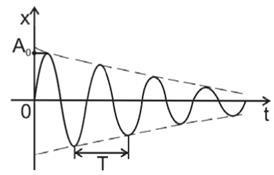
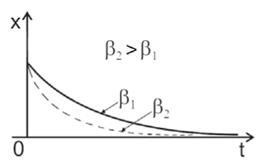
7.6 ábra - A csillapított oszcillációk jellemzői
A rugós inga csillapított mechanikai rezgése két erő hatására történik: a rugalmasság ereje és az ellenállási erő:
ahol r az ellenállás együtthatója.
Newton második törvényének egyenletével:
Az utolsó egyenletet m-vel osztjuk meg, és bemutatjuk a jelölést vagy
ahol # 946; a csillapítási együtthatót, akkor az egyenlet a forma
Ez a kifejezés a csillapított oszcillációk differenciál egyenlete. Az egyenlet megoldása:
Ez a csillapított oszcilláció exponenciális jellegét jelenti, azaz Az oszcillációk amplitúdója exponenciálisan csökken (7.6. Ábra):
Az oszcillációk amplitúdójának relatív csökkenését egy adott periódus alatt egy csillapítási csökkenés jellemzi
vagy a csillapítás logaritmikus csökkenése:
Csillapítási tényező # 946; fordítottan arányos az idővel # 964; amelynek során az oszcillációk amplitúdója e-szeresére csökken:
A csillapított rezgések frekvenciája mindig kisebb, mint a természetes oszcillációk gyakorisága, és a kifejezésből is
ahol # 969; 0 a rendszer természetes oszcillációinak gyakorisága.
Ennek megfelelően a csillapított oszcillációk időtartama:
A súrlódás fokozódásával az oszcillációs periódus nő, és idővel.
A csillapítatlan rezgések szükség további változó hatása a külső erő, ami nyomja a anyagi pont az egyik irányba, majd a másik, és a művelet, amelynek lenne pótolni folyamatosan csökkenteni fordított energia leküzdésében súrlódás. Egy ilyen változó erőt kötelező erőnek neveznek. A fellépés során fellépő csillapodó rezgéseket kényszerítették.
Ha a hajtóerő a kifejezésnek megfelelően változik, akkor a kényszerített oszcilláció egyenlet formát ölt
ahol # 969, a hajtóerő ciklikus frekvenciája.
Ez a kényszerkiválások differenciál egyenlete. A megoldás formában írható
Az egyenlet a hajtóerő frekvenciájával egyenlő frekvencián fellépő harmonikus oszcillációt írja le, amely fázisban különbözik # 966, az erő oszcillációjáról.
A kényszer oszcilláció amplitúdója:
Az erő és a rendszer oszcillációi közötti fáziskülönbség az expresszióból származik
A kényszerített oszcilláció grafikonját a 7.7 ábra mutatja.
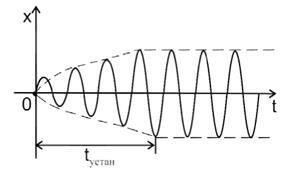
7.7. Ábra - Kényszerített oszcillációk
A kényszerített oszcillációk esetében előfordulhat olyan jelenség, mint a rezonancia. A rezonancia a rendszer oszcillációinak amplitúdója.
Meghatározzuk azt a feltételt, amely alatt rezonancia keletkezik, ezért figyelembe vesszük az egyenletet (7.30). Lássuk az állapotot, amellyel az amplitúdó a maximális értéket feltételezi.
A matematikából ismert, hogy egy függvény végső értéke akkor lesz, ha a származék nulla, azaz.
Az átalakulás után kapunk
Ezért - a rezonáns frekvencia.
A legegyszerűbb esetben a rezonancia akkor fordul elő, ha a külső F időszakos erő F frekvenciával változik # 969; egyenlő a rendszer természetes oszcillációinak gyakoriságával # 969; = # 969; 0.
Az oszcillációk terjedésének folyamatát egy folyamatos közegben, időben és térben periodikusan hullámprocesszivá vagy hullámnak nevezik.
Amikor a hullám elterjed, a közeg részecskéi nem mozognak a hullámmal, hanem oszcillálnak az egyensúlyi helyzetük közelében. A részecske hullámával együtt a közeg részecskeihez csak a vibrációs mozgás állapotát és energiáját továbbítják. Ezért a hullámok fő tulajdonsága, természetétől függetlenül, az energia átadása az anyag átadása nélkül.
Az alábbi típusú hullámok különböztethetők meg:
A rugalmas (vagy mechanikus) hullámokat elasztikus közegben elterjedő mechanikai zavaroknak nevezzük. Minden rugalmas hullámban egyszerre kétféle mozgás van: a közeg részecskéinek oszcillációja és a perturbáció terjedése.
Olyan hullám, amelyben a közeg részecskéinek vibrációja és a hullám terjedése egy irányban történik, hosszirányúnak nevezik. és egy hullám, amelyben a közeg részecskéi merőlegesek a hullám terjedésének irányára, keresztirányúnak nevezik.
A hosszanti hullámok olyan táptalajban mozoghatnak, amelyben rugalmas erők merülnek fel a nyomás és a feszültség deformációi között, azaz szilárd, folyékony és gáznemű testek. A keresztirányú hullámok olyan táptalajban mozoghatnak, amelyben rugalmas erők merülnek fel a nyírási deformáció során, azaz szilárd anyagokban. Így folyadékokban és gázokban csak hosszanti hullámok jelennek meg, és szilárd anyagokban - mind hosszanti, mind keresztirányban.
A rugalmas hullámot szinuszos (vagy harmonikusnak) nevezik, ha a közeg részecskéinek megfelelő rezgései harmonikusak.
A legközelebbi részecskék közötti távolságot, ugyanabban a fázisban oszcillálva, a hullámhossznak nevezzük # 955; .
A hullámhossz megegyezik azzal a távolsággal, amelyhez a hullám az oszcilláció periódusaival egyenlő időben terjed.
ahol a hullám terjedési sebessége.
Mivel (hol # 957; az oszcilláció frekvenciája), akkor
Azok a pontok geometriai helyzete, amelyekhez az oszcilláció eléri a t időtartamot. az úgynevezett hullámfront. Az azonos fázisban oszcilláló pontok geometriai helyét hullámfelületnek nevezzük.
A hullámok olyan hullámok, amelyek a térben energiát hordoznak. Egy hullámhossz egyenletének levezetéséhez - az oszcilláló pont eltolódásának függvénye a koordinátán és az időben - az x tengely mentén terjedő sík szinuszos hullámot veszi figyelembe.
Tegyük fel, hogy a környezet O pontján valamilyen rezgésforrás van:
Egy bizonyos B. pontban, amely a forrásból x távolságra található,
az oszcilláció időben elmarad az O ponton lévõ oszcillációktól. Mivel a hullám az x távolság eléréséhez szükséges. ahol a hullám terjedési sebessége.
Az oszcillációk egyenlete a B pontban lesz
Azóta
A szubsztitúció után az x tengely mentén hullám hullámegyenlete:
A hullámok elméletében a hullámvektor fogalmát használjuk:
A hullámvektor abszolút értéke megegyezik a 2π szegmens hullámhosszainak számával. A hullámvektor az űrben irányult a hullámterjedés irányában.
Általában az x tengely mentén térben terjedő úton lévő hullám egyenlete. van a formája
hol van a hullámszám, a fázis sebesség, vagy a hullám terjedési sebessége
A fázis sebesség függ a frekvenciától
Ebben az esetben a hullámegyenletnek megvan a formája
Ezt az egyenletet sík és gömbös hullámok elégítik ki.