A többcélú (vektor) optimalizálás problémájának megfogalmazása
Lexikográfiai kritérium
Olyan helyzet, amelyben a rendezett kritériumok közötti különbség olyan nagy, hogy a soron következő kritérium csak akkor tekinthető csak akkor, ha az összehasonlított alternatívák megkülönböztethetetlenek a legmagasabb kritériumokkal. Ezt a választást az alternatívák lexikográfiai rendezésének nevezték, mivel ezt a módszert használják, amikor szavakat rendelnek különböző szótárakhoz. Leggyakrabban az MH olyan fontos szigorú rendezéssel, hogy fontos szempontok merülnek fel, amikor további kritériumok szekvenciális bevezetését a szokásos skalár optimalizációs problémákba sorolják, amelyek nem egységesek lehetnek. Tegyük fel például, hogy egy F1 kritériummal kapcsolatos problémának több megoldása van. Ilyen helyzet gyakran felmerül a lineáris programozás, a diszkrét programozás problémáiban. Ebben az esetben a végső választásnál használhatjuk a második, további F2 kritériumot, és olyan megoldást kereshetünk, amely minimalizálja az F1 kritériumot, és megadja az F2 kritériumnak a legkisebb értéket. Ha a második kritérium nem tartalmaz egyetlen megoldást, akkor megadhatja a harmadik F3 kritériumot stb.
A részleges kritériumok egyenlőségének módszere
A kritériumok a kompromisszum elvén dolgoznak, az egységesség eszméjén alapulva. Az egységes kompromisszum ötlete alapján megpróbálják megtalálni az X változók olyan értékeit, amelyeknél az összes kritérium normalizált értékei egyenlővé válnak egymással, azaz
Figyelembe véve az egyes kritériumok fontossága súlyösszetevőit, a kifejezés (3) formában is megírható
Helyettes. Számos speciális kritérium alapján, a kapcsolatok bonyolultsága miatt néha nehéz elérni (3) és (4).
A Bayes-Laplace kritérium
Ez a kritérium azt feltételezi, hogy a lehetséges természeti állapotokhoz valószínûsíthetõ az elõfordulásuk egy bizonyos valószínûsége, és miután meghatározta a gyõzelmek matematikai várakozását minden egyes döntéshez, válassza ki azt a nyereményt, amely a nyeremény legnagyobb értékét adja:
A Bayes-Laplace-kritérium a következő követelményeket határozza meg a döntéshozatalhoz:
a Bj államok előfordulási valószínűsége ismert, és nem függ az időtől;
a megoldás megvalósul (elméletileg) végtelenül sokszor;
A megoldás kisszámú megvalósításához bizonyos kockázatok megengedettek.
A fő kritérium módszere. Lexikográfiai kritérium
A fő kritérium módszer
Van egy gyakori módja, hogy csökkentsék a probléma, hogy egy multi-kritériumok egyetlen kritérium - az, hogy válassza ki az egyik (fő, fő) kritériumok F1 és kérje a fizetést maximum (minimum), és a többi F2. F3. Az Fm részleges kritériumok csak bizonyos korlátozásokat írnak elő, és nem kevésbé (nagyobbak), mint bizonyos értékek.
Olyan helyzet, amelyben a rendezett kritériumok közötti különbség olyan nagy, hogy a soron következő kritérium csak akkor tekinthető csak akkor, ha az összehasonlított alternatívák megkülönböztethetetlenek a legmagasabb kritériumokkal. Ezt a választást az alternatívák lexikográfiai rendezésének nevezték, mivel ezt a módszert használják, amikor szavakat rendelnek különböző szótárakhoz. Leggyakrabban az MH olyan fontos szigorú rendezéssel, hogy fontos szempontok merülnek fel, amikor további kritériumok szekvenciális bevezetését a szokásos skalár optimalizációs problémákba sorolják, amelyek nem egységesek lehetnek. Tegyük fel például, hogy egy F1 kritériummal kapcsolatos problémának több megoldása van. Ilyen helyzet gyakran felmerül a lineáris programozás, a diszkrét programozás problémáiban. Ebben az esetben a végső választásnál használhatjuk a második, további F2 kritériumot, és olyan megoldást kereshetünk, amely minimalizálja az F1 kritériumot, és megadja az F2 kritériumnak a legkisebb értéket. Ha a második kritérium nem tartalmaz egyetlen megoldást, akkor megadhatja a harmadik F3 kritériumot stb.
A kockázatvállalás veszélye a kísérlet lehetőségével
Egy fa, amely felsorolja a döntéshozatali folyamat összes lépését - a döntési fa. A fa ágai a lehetséges alternatíváknak felelnek meg, és a csúcsok megfelelnek a feltörekvő helyzeteknek. Azokat a pozíciókat, amelyekben a mozgást a csoport vezetője végzi, egy téglalap képviseli; a helyzet, amelyben a természet mozog, egy kör.
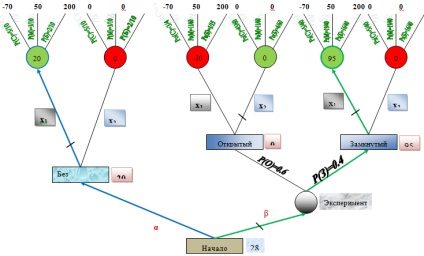
A játék a következőképpen alakul. A kiindulási helyzetben a kört a csapatvezető végzi. Határozatot kell tennie - α vagy β. Ha elhagyta a kísérletet, a játék a következő pozícióba kerül, ahol a csapatvezetőnek el kell döntenie: x1 vagy x2. Ha úgy dönt, hogy végezzen egy kísérletet, a játék mozog a helyzetbe, amelyben a természet rendje nem választotta egyik államok O vagy H, megfelelő a lehetséges következményeket a kísérlet, és így tovább. D. A játék akkor ér véget, amikor az belép a végleges helyére (azaz. a fa csúcsa).
2. lépés Minden döntésre, amely a természet folyománya, meg kell találnunk ennek a lépésnek a valószínűségét. Ha ez a sor jellegű út, amely összeköti azt a kezdeti helyzetbe, áthalad a helyzet (E) azt jelenti, hogy végezzen a kísérlet, az állami valószínűségek P (G) P (M) és a P (B) feltétel nélküli (doopytnymi).
Ha a természet pozíciójához a kiindulási helyzethez csatlakozó út áthalad az (E) pozíción, akkor a környezetállapotok valószínűsége feltételes valószínűséggé válik, és a képletek találják.
3. lépés: A játékfa összes pozícióját kiértékeljük, "lefelé" a véghelyzetből kiindulási helyzetbe. A pozícióbecslés a várható nyereség ebben a pozícióban.
Minden pozícióban a játékos a fa ágát egy kötőjelrel jelöli, ami a maximális pontszámot elérő pozícióhoz vezet.
Oh
Kísérlet nélkül. Válassza ki a maximális értéket (20, 0). 20-nak felel meg.
Vessünk egy pillantást a Fig. 1. A kiindulási helyzetben a kísérlet nélküli (α alternatív) nyereség 20 egység; a várható profit a kísérlet (alternatív β) - 28 egység. Ezért célszerű dönteni - kísérletet végezni (szeizmikus kutatás). Továbbá, ha a kísérlet azt mutatja, hogy a talaj nyitva van, akkor a fúrást nem szabad elvégezni, de ha le van zárva, fúrni kell.
2 - ág: 0
3
A kísérlet.
A maximális értéket választjuk ki
(-30, 0, 95, 0). Ez megegyezik a 95-ös értékkel.
- ág:? ? = -30
6 - ág: 0
Amint az a probléma állapotából következik, 95 egységnyi értéket kaphatunk 0,4 valószínűséggel. Ezért a várható nyereség 0,4 * 95 = 38 egység. Vonja le a kísérlet költségeit 10 egységgel. Végül 28 egység kap.
Súlyösszetevők. A súlyozási együtthatók meghatározására szolgáló módszerek
A rangsorolás módja. Minden szakértőt arra kérik, hogy fontolja meg a tervezett objektum sajátos kritériumait. Az első szám a legfontosabb kritérium, a második pedig a következő fontos kritérium, és így tovább.
, i = 1,2, ..., m.
- (i = 1,2, m) az i súlyozási együtthatók kiszámítására szolgáló képlet.
Pontozási módszer
Ez a módszer arra a tényre épül, hogy a szakértők egy adott kritérium fontosságát egy [0-10] skálán mérik. Megengedhetjük, hogy értékeljük a törtszámú mennyiségek fontosságát, vagy hogy a kiválasztott skálaból ugyanazt a értéket több kritériumhoz rendeljük.
hol van az i-edik sor sorszáma.
rik - az i-edik szakértőnek a k-kritériumra kiszámított súlyát nevezik. Ezért figyelembe véve ezt
Problémák a vektor optimalizálási problémák megoldásában
Normalizációs kritériumok. Mivel a részleges kritériumok eltérő fizikai értelemben különböző mértékegységekben mérve; méreteik nem mérhetőek, ezért nem lehet összehasonlítani az egyes kritériumok eredményeinek minőségét. A helyi kritériumok méretarányának egyetlen, általában dimenzió nélküli csökkentését a normák normalizálásának nevezik.
Az optimalitás elve kiválasztása, pl. Szükséges egy olyan szabály meghatározása, amely lehetővé teszi számunkra, hogy megmondjuk, melyik megoldás jobb. Az optimalitás elve a vektor optimalizálásának fő problémája.
Számviteli prioritási kritériumok. Általában a probléma fizikai jelentőségéből következik, hogy a helyi kritériumok eltérő jelentőséggel bírnak a probléma megoldásában, azaz az egyik helyi kritérium elsőbbséget élvez egy másik helyi kritériummal szemben. Ezt figyelembe kell venni az optimális elv megválasztásánál és a lehetséges megoldások alkalmazási körének meghatározásánál, fontosabb kritériumokat előnyben részesítve.
A ZVO optimális számítása. Most bizonyos előrelépés történt a matematikai programozási problémák (MP) megoldásában. Így egyes források szerint, egy kritérium optimalizálási módszerek és azok módosításainak több mint ötszáz (500), a másik - számuk meghaladta a néhány ezer! De általában nem alkalmazhatók egyenként a ZMO megoldására, t. vannak példák, amikor a számítógépes algoritmusok alkalmatlanok megoldására MP problémák miatt kis változtatások és kiegészítések az eredeti problémát, így van egy probléma - a számítás az optimális előállított vektort optimalizálási probléma. Megjegyezzük azonban, hogy a felsorolt problémák valahogy csökkentik a többváltozós problémát az egy kritériumra, azaz csökkenti az optimum kiszámításának problémáját.
A ZVO megoldásának módszereinek fejlődése három irányban megy végbe:
A vektor kritériumának skálázása egy skalár kritériummal, azaz. átmenet egy objektív optimalizálási problémára;
Az egy objektív problémák véges sorának következetes megoldása;
A D készlet szűkítése az optimális megoldás közvetlen kiválasztásával.