A poláris koordinátarendszer alapkoncepciói és példái
A polár koordinátarendszerben definiáljuk egy pont megadásával O. úgynevezett pólus származó ezen a ponton gerenda OA (jelöljük úgy is, mint Ox), említett a sarki tengely, és megváltoztathatja a skála hosszúságú. Ezenkívül a polárkoordinátarendszer meghatározásakor meg kell határozni, hogy az O pont körüli körforgás pozitívnak tekinthető (a rajzokon az óramutató járásával ellentétes irányú fordulatok általában pozitívnak tekintendők).
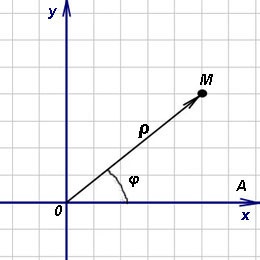
Tehát a síkon (fent) egy O pontot (pólust) és néhány sugárnyit választunk ki. Emellett a mértékegységet is jelezzük. A poláris pont koordinátáit M nevezzük két szám ρ és φ, amelyek közül az első (A polársugár ρ) az a távolság M pont és a második pólus O. (polárszög φ, amely más néven amplitúdó) - a szög, amellyel kell forgatni az óramutató járásával ellentétes gerenda Ox-et, mielőtt az OM-sugárhoz igazodna.
Az M pontot a ρ és φ poláris koordinátákkal az M (ρ, φ) szimbólum jelöli.
Megállapítjuk a kapcsolatot a pont poláris koordinátái és a Descartes-koordináta között. Feltételezzük, hogy a derékszögű téglalap alakú koordinátarendszer kezdete a pólusban van, és az abszcissza pozitív félszekvenciája egybeesik a poláris tengellyel. Adjuk meg az M pontot az x és y karteias koordinátákkal és a ρ és φ poláris koordinátákkal
Az M pont ρ és φ poláris koordinátáit a következõ: Descartes-koordináták alapján határozzuk meg:
Annak érdekében, hogy megtaláljuk a φ szög értékét, szükség van az x és y jelek használatára. határozza meg azt a kvadrátot, amelyben az M pont található, és emellett kihasználja azt a tényt, hogy a φ szög érintője egyenlő.
A fenti képleteket a rendszámtani koordinátákról a polárisokra való átmenet képleteként nevezik.
1. példa Poláris koordináta-rendszerben a pontokat
Keressük meg azokat a pontok poláris koordinátáit, amelyek szimmetrikusak ezeknek a pontoknak a poláris tengelyhez viszonyítva.
A megoldás. Szimmetriával a sugár hossza nem változik. Ezért az első koordináta - a sugár hossza - a poláris tengely körül szimmetrikus ponttal megegyezik egy adott ponttal. Amint az a lecke elején látható ábrából látható, amikor egy pontot állít elő, amely szimmetrikus a poláris tengely körül, ezt a pontot a pólus tengely körül ugyanazzal a szöggel kell forgatni. Ezért a poláris koordinátarendszerben a szimmetrikus pont második koordinátája az eredeti pont szöge, amelyet az ellenkező jelkel vettünk, vagyis -φ. Így egy adott poláris tengelyhez szimmetrikus pont poláris koordinátái csak a második koordinátában különböznek egymástól, és ez a koordináta a jelhez képest ellentétes lesz. A szükséges szimmetrikus pontok poláris koordinátái a következők:
2. példa Poláris koordináta-rendszerben a pontokat
Keressük meg a pólusokhoz képest ezekkel a pontokkal szimmetrikus pontok poláris koordinátáit.
A megoldás. Szimmetriával a sugár hossza nem változik. Ennek következtében az első koordináta a sugár hossza, mivel egy pólusra szimmetrikus pont ugyanaz, mint egy adott pont esetében. A pólushoz képest szimmetrikus pontot úgy kapjuk meg, hogy a kiindulási pontot 180 ° -kal elforgatjuk az óramutató járásával ellentétes irányban, vagyis egy π szöggel. Következésképpen, a második koordináta pont szimmetrikus az adott pólus számítjuk φ + π (ha az eredmény, a számláló felett nevező majd vonjuk ki a kapott száma egy teljes fordulattal, azaz 2π). A pólusokhoz szimmetrikus pontok alábbi koordinátáit kapjuk:
3. példa A poláris koordináta rendszer pólusa egybeesik a kartezián téglalap alakú koordináták kezdetével, és a poláris tengely egybeesik az abszcisák pozitív félévével. A poláris koordinátarendszerben pontokat kapunk
Keresse meg a pontok Descartes-koordinátáit.
A megoldás. A poláris koordinátákról a karteziusiakra való átmenet formuláit használjuk:
Ezeknek a pontoknak a következő Descartes-koordinátáit kapjuk:
4. példa A poláris koordinátarendszer pólusa egybeesik a Descartes téglalap alakú koordináták kezdetével, és a poláris tengely egybeesik az abszcissza pozitív szemiaxisával. Karteziánus négyszög koordináta rendszerben, pontok
Keresse meg ezeknek a pontoknak a poláris koordinátáit.
A megoldás. Határozzuk meg az első poláris koordinátákat a képlet segítségével, és a φ szög érintője a poláris koordináták második. Szerezd meg a következő pontok poláris koordinátáit: