Képes Wikipedia ellipszis

Fogalommeghatározás [| ]

Az ellipszis az Euklideszi sík M pontjának helye. amelyre az F 1> és F 2> pontokra (fókokra) megadott távolságok összege állandó és nagyobb, mint a fókák közötti távolság, azaz

Kapcsolódó meghatározások [| ]

• Az ellipszis gömbökön keresztül haladva az AB szegmenst, amelynek végei ellipszisre helyezkednek, ezt az ellipszis fő tengelyét nevezik. A fő tengely hossza 2 a a fenti egyenletben.
• Az ellipszis fő tengelyére merőleges CD-szegmens a fő tengely központi pontján áthaladva, amelynek végei ellipszisre helyezkednek, az ellipszis kisebb tengelye.
• Az ellipszis nagy és kis tengelyeinek metszéspontját központnak nevezik.
• Az ellipszis középpontjától a nagy és kis tengelyek csúcsaihoz húzódó szegmenseket az ellipszis semimajor tengelyének és semimajor tengelyének nevezzük, és azokat a és b jelöli.
• Az ellipszis egyik pontján lévő r 1> és r 2> távolságokat fókusz sugárnak nevezzük.
• A c = | távolság F 1 F 2 | 2 F_ | >>> a fókusztávolságnak nevezzük.
• A mennyiség e = c a = 1 # x2212; b 2 a 2> = >>>>>> nevezzük excentricitást.
• Az ellipszis átmérőjét önkényes akkordnak nevezik, amely áthalad a központján. Az ellipszis konjugátumátmérőit egy pár átmérőjének nevezik, amelyeknek a következő tulajdonsága van: az első átmérőkkel párhuzamos akkordok középső része a második átmérőn van. Ebben az esetben a második átmérővel párhuzamos akkordok középpontja az első átmérőn van.
• Az ellipszis sugara egy adott ponton az a szegmens, amely összeköti az ellipszis középpontját a ponttal, és annak hossza is, amelyet a következő képletből számítunk: r = a b b 2 cos 2 # x2061; # x03C6; + a 2 bűn 2 # x2061; # x03C6; = b 1 # x2212; e 2 cos 2 # x2061; # x03C6; \ cos ^ \ varphi + a ^ \ sin ^ \ varphi >>> = \ cos ^ \ varphi >>>>. ahol # x03C6; - a sugár és a semimajor tengely közötti szög.
• A p = b 2 a >>> fókuszparaméter az akkord félhosszúsága. a fókuszon átmenő és az ellipszis fő tengelyére merőleges.
• A kis és nagy félévek hosszának arányát az ellipszis vagy ellipticitás kompressziójának együtthatójaként nevezik. k = b a.>.> Az érték egyenlő (1 # x2212; k) = a # x2212; b a.>,> az ellipszis összehúzódásának nevezzük. Körhöz a tömörítési arány megegyezik az egységgel és a kontrakció nullára. Az ellipszis kompressziós együtthatója és excentricitása a k 2 = 1 relációval függ össze # x2212; e 2 = 1-e ^.>
• Minden egyes golyó esetében van egy line, amit directrix-nek hívnak. oly módon, hogy az ellipszis tetszőleges pontjától a fókuszhoz viszonyított távolság és az adott ponttól az adott pontig terjedő távolság egyenlő legyen az ellipszis excentricitásával. Az egész ellipszis az egyenes vonal ugyanazon oldalán fekszik, mint a fókusz. Az ellipszis direktrix egyenleteit a kanonikus formában x = # x00B1; p e (1 + e) ​​>> a foci ( # x2213; p 1 + e. 0)>, \, 0 \ jobb)>. A fókusz és a rendező közötti távolság p>.>

Az ellipszis elemei közötti kapcsolat [| ]

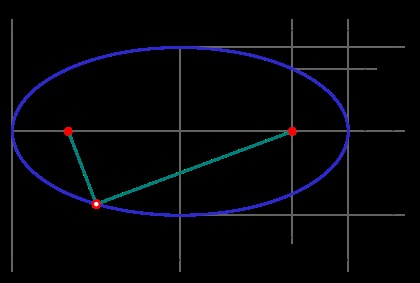
Az ellipszis részei (leírás, lásd "Kapcsolódó meghatározások")

Ellipszis a második rend görbévé [| ]

Az ellipszis a második rend központi nem degenerált görbéje és megfelel a forma általános egyenletének

egy 11 x 2 + 22 y 2 + 12 x 2 y 2 + 13 x 2 + 23 + 33 y = 0. x ^ + a_y ^ + 2a_xy + 2a_x + 2a_y + A_ = 0,>

A második rend görbéjének invariánsai és az ellipszis félévek közötti kapcsolat (csak akkor igaz, ha az ellipszis középpontja egybeesik az eredettel és egy 33 = # x2212; 1 = -1>):

Ha átírjuk az általános egyenletet a formában

A X 2 + B X Y + C Y 2 + D X + E Y + F = 0. + BXY + CY ^ + DX + EY + F = 0,

akkor az ellipszis középpontjának koordinátái:

A forgási szöget az expresszió határozza meg

A tengelyvektorok iránya:

A félévek hosszát kifejezésekkel adjuk meg

Fordított arány - általános egyenlete együtthatói ellipszis paramétereinek - úgy állíthatjuk elő, helyettesítve a kanonikus egyenlet (lásd alább.) Expression forgatni a koordinátarendszert szögben Θ és transzfer a pont (x c y c.), Y _)>:

x # x2032; 2 a 2 + y # x2032; 2 b 2 = 1 >>> + >>> = 1> x # x2032; = (x # x2212; x c) c o s # x0398; + (y # x2212; y c) s i n # x0398; ) cos \ Theta + (y-y_) sin \ Theta> y # x2032; = # x2212; (x # x2212; x c) s i n # x0398; + (y # x2212; y c) c o s # x0398; ) sin \ Theta + (y-y_) cos \ Theta>

A helyettesítést és a zárójelek megnyitását a következő egyenleteket kapjuk az általános egyenlet koefficienseihez:

A = a 2 (s i n # x0398; ) 2 + b 2 (c o s # x0398; ) 2 (sin \ Theta) ^ + b ^ (cos \ Theta) ^> B = 2 (b 2 # x2212; a 2) s i n # x0398; c o s # x0398; -a ^) sin \ Theta cos \ Theta> C = a 2 (c o s # x0398; ) 2 + b 2 (s i n # x0398; ) 2 (cos \ Theta) ^ + b ^ (sin \ Theta) ^> D = # x2212; 2 A x c # x2212; B y c -By_> E = # x2212; B x c # x2212; 2 C y c -2Cy> F = A x c 2 + C y c 2 + B x c y c # x2212; a 2b2 ^ + Cy_ ^ + Bx_y_-a ^ b ^>

Ha csak a szöget adja meg és elhagyja az ellipszis középpontját,

Meg kell jegyezni, hogy az egyenletben az általános formája egy ellipszis meghatározott derékszögű koordinátarendszerben, az együtthatók ABCDE F (vagy ezzel ekvivalens, a 11. 2 12. A 22. 2 a 13. 2 33 a 23., 2a_, A_, 2a_, 2a_, a_>) vannak meghatározva, akár egy tetszőleges konstans faktorral, azaz a fenti bejegyzés és

A k X 2 + B k X Y + C k Y 2 + D k X + E k Y + F k = 0 + BkXY + CkY ^ + DkX + EkY + Fk = 0>

ahol k # x2260; 0. egyenértékűek. Nem várható ez a kifejezés

minden k esetében végrehajtásra kerül.

Az invariáns I és semiaxek közötti kapcsolat általános formában a következő:

ahol F # x2032; = F # x22C5; (A # x22C5; h 2 + B # x22C5; h # x22C5; k + C # x22C5; k 2 # x2212; 1) + B \ cdot h \ cdot k + C \ cdot k ^ -1)> az F együttható, amikor az eredetet az ellipszis középpontjába mozgatja, amikor az egyenletet az alakra

Az egyéb invariánsok a következő kapcsolatokban vannak:

A kanonikus egyenlet [| ]

Minden ellipszis számára egy Descartes-koordináta-rendszert találunk, amellyel az ellipszist az alábbi egyenlet írja le:

Ezt az egyenletet ellipszis kanonikus egyenletének nevezik. Ellipszist ír le a kiindulási központtal, amelynek tengelyei egybeesnek a koordinátatengelyekkel. [1]

A definitás érdekében 0-ot állítunk be

Az ellipszis féltengelyének ismeretében kiszámíthatja fókusztávolságát és excentricitását:

Ellipszis foci koordinátái:

Az ellipszisnek két direktrixja van, amelyek egyenleteit írhatjuk

A fókuszparaméter (azaz a fókuszon átmenő, az ellipszis tengelyére merőleges fül hossza fele) egyenlő:

Fókusz sugarak, vagyis a gömbök távolsága a görbe tetszőleges pontjához (x Y).

Az átmérő egyenlete. konjugált akkord k szöghatárral. :

Az ellipszis pontján (x 0 y 0), y _)> lévő érintő egyenlete egyenletes.

Az adott szögszögű tangensek egyenlete k:

az ilyen egyenes ellipszis pontossági pontjai (vagy ugyanazon az ellipszis pontjai, ahol az érintő szögben van a k érintővel):