Szekvenciális oszcilláló áramkör - stadopedia
Rezonancia jelenségek az elektromos áramkörökben
Soros oszcilláló áramkör használata
Energiakapcsolatok egy soros oszcilláló áramkörben rezonancián
A jelforrás belső ellenállásának hatása az áramkör frekvenciaválaszára
Szekvenciális oszcilláló áramkör
Rezonancia jelenségek az elektromos áramkörökben
Egymást követő vibrációs áramkör
Az elektromos áramkör rezonanciája a reaktancia eltűnésének jelensége. Az effektus gyakoriságát rezonánsnak hívják. A rezonancia csak olyan áramkörökben fordulhat elő, amelyeknek legalább egy különböző típusú vezetőképességű reaktív eleme van.
A rezonanciák mind az elektromos áramkör különálló ágaiban, mind a kontúrokban játszhatók le. Ezért különböző típusú reaktív elemekkel rendelkező áramkörökben több rezonáns frekvencia is lehet.
A rádiós technikában az elektromos áramkörök rezonanciajelenségeit széles körben használják a frekvenciasáv elkülönítésére és a jelek erősítésére.
Az elemek soros összekapcsolásával ellátott láncot szekvenciális oszcilláló áramkörnek nevezik. Mivel a valós induktivitások és kapacitások veszteségeket mutatnak, ezt figyelembe veszik a sorozatban lévő áramkörrel, kis veszteségállósággal (15.1. Ábra).
Ennek az áramkörnek az impedanciája lesz
ahol - a modul, és - az aktív és reaktív komponensek, - az impedancia fázisa.
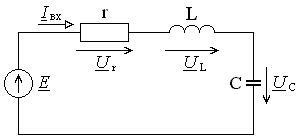
Ábra. 15.1. Szekvenciális oszcilláló áramkör
A rezonáns frekvencián az impedancia reaktív komponense eltűnik, vagyis állapot
Ezért a rezonáns frekvencia kiszámításához egy képletet kapunk a sorozat oszcilláló áramkörének paraméterei alapján
Kevésbé rezonáns frekvenciákon az áramkör reaktanciája negatív, azaz kapacitív jellegű, mivel a kapacitás-ellenállás nagyobb, mint az induktivitás-ellenállás és domináns. A rezonancianél nagyobb frekvenciákon a sorozatú oszcillátor áramkör reaktanciája pozitív, induktív jellegű, mivel ebben az esetben az induktivitás ellenállása nagyobb lesz, mint a kapacitív ellenállás.
A kifejezést (15.1) a rezonáns frekvencia bevezetett koncepciójával biztosítjuk:
Az ellenállás mérete az áramkör hullámát vagy jellegzetes impedanciáját jelenti, és
A veszteségek ellenállásának jellemző ellenállásának arányát az áramkör Q-tényezőjének nevezik, amelyet a szimbólum és a csillapítás kölcsönhatása jelez:
A rossz minőségű kontúrok minőségi tényezője kisebb, mint 50. A közepes minőségű áramkörök esetében az arány megfelel a jó minőségű áramköröknek és a kiváló minőségű áramköröknek.
A (15.4) képletben a zárójelben lévő kifejezés görög betűvel van jelölve, és a relatív kontúr
Értelemszerűen a relatív detonáció relatív egységekben jellemzi a jelforrás frekvenciájának eltérését az áramkör rezonancia frekvenciájából.
Figyelembe véve a bevezetett jelölést, a rezisztencia formula (15.4) kompakt formában írható:
Az áramkör áramköre az Ohm törvényében található meg:
ahol az emf forrás kezdeti fázisa, az impedancia fázisa egy másik rögzítési formában.
A rezonancia frekvencián az áram maximális és egyenlő
A normalizált amplitúdófrekvencia (AFC)
és a fázisfrekvencia jellemzői (PFC)
az 1. ábrán látható. 15.2.
A rezonáns frekvencián a relatív detuning (15.7) nulla. ezért
Következésképpen a rezonanciafrekvencián az induktivitás és a kapacitás feszültségének amplitúdója megegyezik egymással, és idővel nagyobb, mint az emf amplitúdója:
Ezért a soros oszcillációs áramkör rezonanciáját a feszültségek rezonanciájának nevezzük. A rezonancia frekvencián az áramkör feszültségének vektordiagramját a 2. ábrán mutatjuk be. 15.3.
Az a frekvenciatartomány, amelynek határainál a jelenlegi érték a maximális értékhez képest időben csökken, az átsáv. Az átjáró határainál a (15.9) képlet szerint feltétel
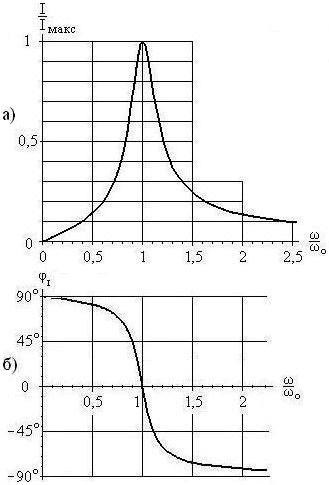
Ábra. 15.2. Amplitúdófrekvencia (a) és fázisfrekvencia (b) áram jellemzői egy sorozat oszcilláló áramkörben
Ábra. 15.3. Soros oszcilláló áramkör vektordiagramja rezonáns frekvencián
Így szerezhetjük meg az átmeneti sáv határain belüli viszonylagos detonáció értékét
Szinte mindig azt feltételezhetjük. Ezért kicsi és nagy hiba nélkül, a (15.7) képlet segítségével, az átviteli sáv határain lévő relatív detonáció kicserélhető hozzávetőleges kifejezéssel:
ahol a a sávszélessége az áramkörnek. A (15.14) és (15.16) kifejezések kombinálásával végül egy meglehetősen pontos képletet kapunk a sávszélesség kiszámításához
A kontúrok egymáshoz viszonyított összehasonlításához kényelmesen használjuk az amplitúdófrekvencia jellemzőket a relatív detonáció függvényében (15.4. Ábra), és nem a relatív frekvencián, mint a 2. ábrán. 15.2.
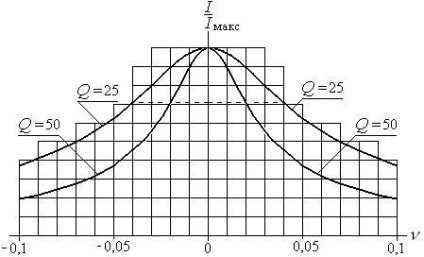
Ábra. 15.4. A sorozat oszcilláló áramkörének amplitúdófrekvencia-jellemzői a relatív detonációtól függően
Meg kell jegyezni, hogy a feszültség a kapacitás
a rezonancia frekvenciájánál kisebb frekvenciánál ér el maximális értéket, és az induktivitáson a feszültség a rezonanciafrekvenciánál nagyobb frekvenciánál nagyobb értéket ér el.