Gauss-gerenda
A csökkentett hullámegyenlet megoldását keresjük. leírva egy ilyen sugár terjedését [1]
ahol u (x, y, z) lassan változó komplex függvény, amely meghatározza a lézersugár tulajdonságait, ami megkülönbözteti a sík hullámtól. A Δ operátort a Ψ függvényre alkalmazzuk
Ha az els˝o származékhoz képest elhanyagoljuk az u u második deriváltját, akkor a redukált Helmholtz-hullám-egyenlet alapján kapjuk meg az egyenletet
A kapott egyenlet parabolikus egyenletekre utal, és a hozzávetőleges közelítést, amellyel a kapott értéket parabolikus közelítésnek nevezzük. Nem nehéz megmutatni, hogy az egyenletet egy Gauss-gerenda fogja kielégíteni, amelynek amplitúdója a keresztirányú koordináta mentén a Gauss-törvénynek megfelelően változik.
Egy Gauss-gerendán írhatunk kifejezést
ahol r 2 = x 2 + y 2. A p paraméter a z-tengely mentén terjedő fény terjedésének komplex fáziseltolódása, és q a komplex gerenda paraméter, amely meghatározza a Gaussian mező eloszlást az r koordinátához képest, ahol r a tengely távolsága. Ezenkívül q határozza meg a hullám elülső oldalának görbületét, amely a tengely közelében gömbölyű.
Vizsgáljuk meg részletesebben egy Gauss-hullám hullámhosszúságú λ tulajdonságait. Ebből a célból a q komplex paramétert az R és a ceruza két valós paramétere alapján fejezzük ki
ahol R a hullámfront görbületi sugara, és w a keresztirányú síkban az E mezőben bekövetkező változást jellemzi (a w paramétert általában a sugárszélességnek nevezik). A mező ezen a síkbeli eloszlása megfelel a Gaussian törvénynek, és w egyenlő azzal a távolsággal, amelynél a mező amplitúdója az e tényezővel csökken a tengely mezőjéhez képest.
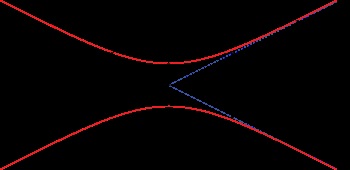
A w (z) Gaussi sugár szélessége z függvényeként. w0. a gerenda nyaka; b. mélységélesség; ZR. a Rayleigh hossza; Θ: a gerenda szögeltérése
Beam szélesség
Egy bizonyos síkban, amelyet caudális felszínnek vagy nyaknak neveznek, a Gauss-gerenda a w0 minimális szélességhez kötődik. Ebben a síkban, ahonnan célszerű számolni a z távolságot, a fázis előlapja sík, és a bonyolult gerenda paraméter tisztán képzelődik
ahol az zR a Rayleigh hossza. Ezután a z távolságon a sugár szélességét a következő képlet adja meg
A görbület sugara
A görbület sugara függ a koordinátától
Sugár divergencia
A w (z) sugárgenerátor egy hiperbola, amelynek aszimptotuma a tengelyhez szögben hajlik
Ez a szög megegyezik az alapmód diffrakciós szögével a távoli mezőben.
A gerenda teljes szögbeli divergenciája
A magasabb megrendelések módjai

Az első kilenc Hermitian-Gauss mód
A Gauss-gerendák csak a paraxiális hullámegyenlet egyik lehetséges megoldásai. Különböző ortogonális megoldások kombinációit használják a lézersugarak szimulálására. Általános esetben, ha a megoldások teljes bázisát definiálják, akkor bármelyik pecsét a megoldások szuperpozíciója lehet.