Digitális integrátor
Integráció a téglalap algoritmussal.
A téglalap algoritmust a különbségegyenlet határozza meg.
Ezt egy rekurzív elsőrendű digitális szűrő valósítja meg (6.14. Ábra, a).
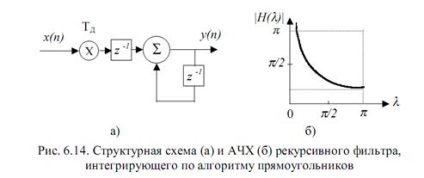
Ezt az átadási jellemző jellemzi. Frekvenciaválasz és szakaszválasz
A szűrőnek van egy nulla az eredetén és egy oszlop az egységkörön. A szűrő potenciálisan instabil.
A beépített integrátor jobban integrálja a trapéz algoritmust, amit a különbségegyenlet határoz meg
Ezt egy rekurzív elsőrendű digitális szűrő hajtja végre (6.15a ábra)
Ezt az átadási jellemző jellemzi. Frekvenciaválasz és szakaszválasz
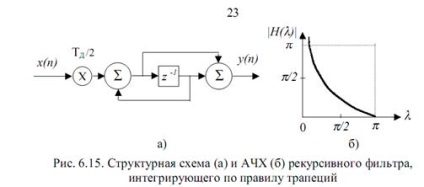
Ezt az átadási jellemző jellemzi. Frekvenciaválasz és szakaszválasz
A szűrőnek van egy nulla a pontján és egy oszlop az egységkörön. A szűrő frekvenciaválaszai elég közel vannak az ideális integrátor frekvenciaválaszához a kevesebb frekvenciánál vagy a szűrő potenciális instabilitása miatt, és az integrációs hiba is idővel megnő.
Digitális integrátor. amely a Simpson szabály szerint működik, a különbségegyenlet alapján történik
A másodrendű megvalósult RF (6. ábra, a6)
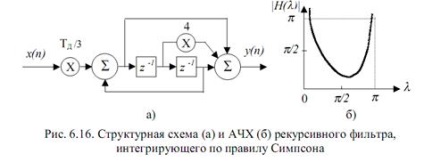
Ezt az átadási jellemző jellemzi. Frekvenciaválasz és szakaszválasz
A szűrőnek egy pár nulja és pólusa van az egységkörön. Ennek a szűrőnek a potenciális instabilitása, amint az a fentiek szerint. a folyamatos integráció korlátozott ideje és annak szükségessége, hogy azt rendszeres időközönként visszahelyezzük az eredeti állapotba, azaz vissza. A szűrő frekvenciaválaszai elég közel vannak az ideális integrátor frekvenciaválaszához a nem magasabb frekvenciáknál. Az ilyen integrátor azonban erősíti a frekvencia zajt. Ezért a trapézszabályozásnak megfelelően jobb a zajos jelek integrálása.