Az üveg szakítószilárdságának elmélete

A merev abszolút test törésének elmélete az üveg szerkezetének elméletéből és a kémiai kötések felszakadásának mechanizmusából áll. A kémiai kötések diszkrét megoszlása ​​üvegben az erõsségük alapján határozza meg az üveg szilárdságát nyújtással. Az üveg szilárdságát a legerősebb kötések ereje jellemzi. A különböző erősségű kötések üvegében való jelenléte előre azt határozza meg, hogy az üveg alacsony szakítószilárdságú anyag.

A szilárd anyagok gyakorlati tulajdonságai közül az erő a legfontosabb. A kristályos szilárd anyagok mechanikai szilárdsága főként a [1] és a [2] struktúrától függ. Az üveg szerkezetének tanulmányozása és az üveges állapot elméletének hiánya komoly nehézségeket okoz az eredmények értelmezésében az üveg mechanikai tulajdonságainak vizsgálata során.

Az üvegben lévő műanyagáramlás lehetetlenségével összefüggésben, még kísérleti adatok hiányában is elméletből következik, hogy az üvegnek kivételes szilárdsággal kell rendelkeznie [5]. Az alacsony szilárdságú üveghez való hozzáállás megváltozott [6], még a magas rugalmasságú üvegek megszerzésének kérdése is [7]. A [4] szerint az üveg nagy természetes erőt képvisel, azonban számos hiba nem teszi lehetővé ezt az erőt.

Annak ellenére, hogy az eddigi nagy szilárdság feltételezhető, a hagyományos technológiák szerint a nagy szilárdságú üvegből nem érkezett meg. Az erősségek problémáján nagy figyelmet fordítanak az üveg elméleti szilárdságának meghatározására. A szerkezet bizonytalanságával összefüggésben az elméleti erőt közvetett módszerekkel értékelték. Az üveg elméleti szilárdsága a becslések szerint 2500 kg / mm2 [8]. Annak ellenére, hogy a hatalmas gyakorlati üveg szilárdsága elméleti szakítószilárdság kicsi, és összege 5-15 kg / mm 2. reprodukáihatatianságát eredmények meghatározásánál a mechanikai szilárdság üveg nem véletlen, de tükrözi a feltételeket a termelés [9].

Az üveg szilárdságát a szerkezet szerkezete, a minta hibái határozzák meg, és nagymértékben függ a vizsgálati körülményektől is. A nehézségek a értelmezése a vizsgálati eredmények a mechanikai szilárdság üvegek társított összetettsége a jelenségek a szakadáskor, amelyek abból erednek, kölcsönhatása számos tényező a minta felvitelekor. Ebben az összefüggésben a szemüvegek tényleges erejének kérdése a hiba és a külső állapotoktól függetlenül fontos, de az anyag szerkezete határozza meg. A szilárd anyagok megsemmisítésének folyamatáról szóló ábrázolások csak a test reakciójának atomi mechanizmusának külső erő hatására történő megfontolásán alapulhatnak. A repedéseket, az inhomogenitást és a szilárd anyagok egyéb hibáit másodlagos tényezőként kell kezelni, amelyek jelentős, és néha meghatározó hatást gyakorolnak az erőre. A hibáknak ez a hatása a szilárd test erejére maszkolja a test saját erejének természetét, amelyet annak szerkezete határoz meg.

Az üveg szilárdságának első elméletét A. Griffiths [10] javasolta. Az üvegpusztítás folyamatának megmagyarázására azt feltételezték, hogy az üvegben vannak mikrotörzsek. Amikor a mintákat a mikrolemezek tetején töltik, túlfeszültség és a kötések későbbi megszakadása következik be. A jelenlét szemüveg legvékonyabb repedések, amelyek az egész minta térfogata, Griffiths magyarázható mismatch technikai és elméleti erejét.

A fő hangsúly Griffith elméletében a mikrotörések jelenlétére utal az üvegben a pusztulás kezdete előtt. Azonban [11] feltételezzük, hogy a repedés megindulása előtt az üvegben nincs mikrotörzs jelenléte, és spontán keletkezhet. A [12] szerint a mikrotömböknek nem feltétlenül kell a szerkezet szerves tulajdonságává válniuk, megjelenésük tisztán véletlenszerű.

Az optikai kvarcüvegek elektronmikroszkópos vizsgálata különféle méretű mikrotömbök formájában, amelyek jelenléte Griffiths feltételezésével nem találtunk [13]. A minta gyártása vagy feltöltése során repedések fordulhatnak elő, azonban a mikrocukrok eredetének kérdése még nem oldódott meg a kimutatásuk megbízható módszereinek hiányában [14].

Az erő statisztikai elmélete abból adódik, hogy az üvegben vannak hibák, amelyek statisztikailag oszlanak el [15, 16]. A minta erejét a legveszélyesebb hiba határozza meg. Ugyanúgy, mint a Griffiths elméletében, a statisztikai elmélet feltételezi a különböző fokú veszélyek hiányát a mintákban.

Ezzel szemben a tisztán mechanikus felfogása szakadása szilárd anyagok az elmúlt évtizedben alakult a koncepció kinetikus megsemmisítése szilárd anyagok [11]. Ennek a koncepciónak a alapjait [17, 18], az atomok termikus mozgásának ötleteiből kiindulva. Egy tömör test megsemmisítését mind az atomok termikus mozgása, mind a mechanikai igénybevételek határozzák meg.

Annak ellenére, hogy sok szemléletű elmélet létezik, a diszkontinuitás molekuláris elméletét még nem hozták létre, és az erőt meghatározó elemi megsértések természetét nem találták meg. Tekintsük az üveg erejét a szerkezetére vonatkozó ötletek alapján. A szerkezet [19] modellje szerint az üvegben a kémiai kötések diszkrét spektruma az erősségük szerint (1.

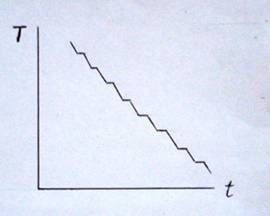
1. ábra Üvegszilárdulák szilárd állapotú fázisátalakulása

hűtés közben és szemüvegek kialakításakor [19].

A hőmérsékleti grafikonon az idő függvényében található minden egyes szerkezeti csoport saját likvidusvonalával rendelkezik. Minél magasabb a strukturális csoport megszilárdulási hőmérséklete, annál több energiát kell megolvasztani. Ezért a szilárd anyag magas hőmérsékletű szerkezeti csoportjai nagyobb szilárdságot mutatnak. Így egy szilárd testben számos szilárdsági szint van a szerkezetben a maximális magas hőmérséklettől a legalacsonyabb alacsony hőmérsékletűekig. A benne lévő üveg kémiai összetételétől függően a diszkrét kötések gyakorisága eltérhet az erejétől, és az azonos szilárdságú kötések száma eltérő lehet.

Az atomok szerkezeti szerkezetétől és a szomszédos atomokkal való kölcsönhatástól függően az egyes atompárok kötődését a merevség és a megengedett relatív megnyúlás jellemzi, amely meghatározza a kötés erejét [20]. Azon az atompárok, amelyek ugyanolyan nyúlással rendelkeznek, mint a kötés ereje.

Az üveg elemi izotróp mikrovolumot veszünk a maradék feszültségek nélkül, és kis húzóerőt alkalmazunk rá. Vizsgáljuk meg az üvegatomok viselkedését a folytonosság jövőbeli síkjában. Minden egyes atompár feszültség alatt áll # 963; = P / n. ahol P - a cselekvõ erõ, n - az atomok száma a mikro térfogat keresztmetszetében. Ahogy a P húzóerő nő, a kémiai kötésekre nehezedő feszültségek növekednek. Ha m-es szint van az adott kémiai összetétel üvegében, akkor n = n 1 + n 2 + ... + n m. ahol n 1 + n 2 + ... + n m az egyes szintek linkjeinek száma. Minden egyes szintre a megengedhető megszakítási feszültségek: # 963; # 963; ... # 963; m. Az üveg abszolút rugalmas, szilárd test, de a szomszédos kémiai kötések természetéből adódó különbség nem lehetséges a műanyag deformációjával [19, 21].

A mikrovolumra ható erő statikus növekedésével a minta keresztmetszetében a szakítószilárdságok elérése minden kötésben legfeljebb # 963; kémiai kötések n 1. elfogadható szakítószilárdságokkal # 963; felrobban. Szerint alkotmányuk atomok törött kötvények egy disszociált állapotban vannak és viszkózus fázisban elasztikus szilárd test [22] .Telo válik viszkoelasztikus, van felelős az erejét a rugalmas szilárd fázis.

A szünet a leggyengébb n 1 jelenleg aktív az üveg microvolumes P erő azonnal újra elosztják a megmaradt csatlakozó n - n 1, és az egyes őket egy kvázi-statikus folyamat egy erő P / (n - n = 1). Azonban, abban az időben a szakadás a leggyengébb n 1 a pillanatnyi terhelés során, amely végzett a törött kötvények a többi ügyek, megjelenik a dinamikus erő komponens tulajdonítható függetlenítés n 1. A teljes hozzáadott teljesítménye a fennmaradó kapcsolatok, tekintettel a dinamikus komponens kétszer akkora erő , amely a leggyengébb kötések szakadására esik [20].

Amikor a leggyengébb kapcsolatok megszakadnak, a rendszer azonnal reagál erre. Az egyensúlyi rendszerben lévő kötések felbomlása a fennmaradó atomok helyének megváltozásához vezet, a rendszer stabilizálása érdekében deformálódik. A húzófeszültség további növelése a feszültségekhez # 963; 2 a csatlakozásnál az n 2 következő szintjei és így tovább, a teljes testtörés megtöréséhez vezet. Így, ahogy a terhelés emelkedése esetén szekvenciális függetlenítését, amelynek folytonos megengedett generált feszültség kisebb hatóerővé és inerciális komponense a törött kötvények. A terhelést azonnal újraosztják a többi linkre.

Vegyük fontolóra, mi képezi a kémiai kötés eltörlésének alapelemét. Szakítószilárdság esetén a gyenge kötések disszociációja kis megengedett nyúlással történik. A gyenge kötések feltörése után a terhelés szoros kapcsolatban van a maximális megengedett nyúlásokkal. A különböző kémiai kötések szakadását jól demonstrálja a mechanikai modell, amikor egymás után egymás után egymás után megszakadnak egymásnak a kötései. Szükség van n különböző hosszúságú szálak vételére, és az ellenkező végüket a csomópontokhoz csatlakoztatni, majd nyújtani őket. Tegyük fel, hogy minden egyes szál megszakad a P. terhelés alatt, akkor egy ilyen rendszert nem pusztít el a Pn erő. de a P. erő

Ha egy üveg mintát nem pusztítanak el, akkor a terhelés eltávolítása után a disszociált kémiai kötések társulnak. A gyenge kötések disszociációjának eredményeképpen helyi mikrotörések csak húzóerővel terhelt üvegben képződnek.

A betöltés előtt és után nincs mikrotörés az üvegben. Nyilvánvalóvá válik, hogy a Griffiths-repedések miért nem kísérletileg észlelhetőek a feszes üvegmintákban. A minta megsemmisítéséhez a gyenge kötvények helyi mikro-töréseinek nincs jelentős értéke. Az üveg szilárdságát nem az összes kémiai kötés erejének összege határozza meg a szakadás síkjában, nem pedig a szerkezeti mikrotömbökön, hanem a legerősebb kötések erejével.

A minta stabilitása a P húzóerő hatására megmarad, ha P < # 963; # 943; (n - n # 943;), azaz van egy bizonyos szintű speciális feszültség a szervezetben # 963; # 943; amelynek terméke a megszakítás nélküli kötések száma meghaladja az aktív hatást. Ha P> # 963; # 943; (n - n # 943;), akkor a testben levő kötések következő szintje elpusztul. Amint fentebb említettük, az erő P dinamikus összetevője az atomkötések megszakításakor # 943; - a második szint növeli a fennmaradó kapcsolatokra ható húzófeszültségeket. Ezért alkotmánya szerint az üveg alacsony szilárdságú anyag, annak ellenére, hogy a fejlődés nem lehetséges a diszlokációkban.

Az üvegtörés folyamata a kémiai kötések szerkezeti csoportjainak állandó erõssége. A leggyengébb linkek feltörése után a terhelést továbbadják a többi linknek. Bár a minta vizuálisan megtartja az élő keresztmetszetet, a leggyengébb kötések elpusztítására képes feszültségek szintjén a terhelés lavina átadása az erő dinamikus összetevőjéből ered, amely megkötötte ezt a kötésszintet más kapcsolatokhoz. Miután az egymás utáni egymás utáni megszakadása erőssége miatt a kötések újbóli feltöltése, amelyek egy bizonyos idő alatt érintetlenek maradtak, azonnali robbanásveszélyes pusztítás következik be. Az üveg kémiai kötéseinek megsemmisítésének mechanizmusa megakadályozza annak alacsony szakítószilárdságát.

1. A merev abszolút rugalmas test megszakadásának elméletét közvetlenül a kémiai kötések szakadásának mechanizmusa fejti ki.

2. A kémiai kötések diszkrét megoszlása ​​az üvegben szilárdságuk alapján határozza meg a szakítószilárdságát.

3. A feszültség alatt álló üvegtörés mechanizmusa a kémiai kötések egymás utáni megszakadása erőssége által a még megszakított kötésekben fellépő feszültségek lavina-szerű növekedése esetén.

4. Az üveg szilárdságát nem az összes kémiai kötés erejének összege határozza meg a szakadás szakaszában, és nem a szerkezeti mikrotömbök, hanem a legerősebb kötések ereje által.

5. A rakott üvegmintában nincs szerkezeti mikrotörzs. Ezek a szakítószilárdságok a gyenge kötések atomjainak disszociációjával keletkeznek. A stresszcsillapítás a gyenge kötések társulásához vezet.

6. A különböző szilárdságú kötések üvegében való jelenléte előreláthatólag azt jelenti, hogy az üveg alacsony szakítószilárdságú anyag.

7. A masszív üveg alacsony szilárdságú, több mint két nagyságrenddel kisebb, mint az elméleti, azt jelzi, hogy a nagy üveg szilárdságú elmélet megalapozásának alapja téves ötlet az üvegről mint amorf testről.

8. Az üveg szerkezetének mint polikristályos, teljesen rugalmas szilárd anyagnak az elméleti struktúrája határozatlan összetételű szerkezeti csoportokkal és különböző mechanikai szilárdságaival magyarázható az ömlesztett üveg alacsony szilárdsága a feszültség szempontjából.

1. C. Huert, R. Thomson. A szilárd anyag fizikája, 142. Mir, M. 1969.

2. GM Bartenev. Ultra erős és nagy szilárdságú szervetlen üvegek, 240. Stroyizdat, M. 1974.

3. IAGoguslavsky. Nagy szilárdságú edzett üveg, 151. Stroiizdat, M. 1969.

4. VPPuh. Az üveg szilárdsága és megsemmisítése, 155. Science, L. 1973.

5. WB Hilling. A könyvben. Üveg szilárdsága, 68. Mir, M. 1969.

6. FF Whitman, AA Bershtein, VPP. A gyűjteményben. Az üveg szilárdsága, 7. Mir, M. 1969.

7. AN Lazarev. A könyvben. Szemüvegek szerkezeti átalakulása magas hőmérsékleten, 233. Nauka, M.-L. 1965.

8. I. Naray-Sabo. A gyűjteményben. Egy üveges állapot, 74. Science, M.-L. 1965.

9. SM Brekhovskikh, VM Kulakov. A könyvben. Mechanikai és termikus tulajdonságok és szervetlen szemüvegek szerkezete, 36. VNIIESM. M. 1972.

10. A. A. Griffith. Phil. Trans. Roy. Soc. 163. szer. A, vol. 221, 587, 1920.

11. SN Zhurkov. Szervetlen sók. Materials, 3, No. 10, 1767, 1967.

12. Ernsberger F.M. A könyvben. Az üveg ereje, 33. Mir, M. 1969.

13. F.K. Aleinikov. DAN USSR, 156, 154, 1964.

14. P.Ya.Bokin. A szilikát üvegek mechanikai tulajdonságai, 180. Nauka, L. 1970.

15. T.A. Kontorova, Ya.I. Frenkel. ZhTF, 11, 173, 1941.

16. B.B.Chechulin. ZhTF, 24, 292, 1954.

17. SN Zhurkov, BN Narzullaev. ZhTF, 23, 1677, 1953.

18. SN Zhurkov. Moskov. AN SSSR, 11, 78, 1957.