Az eredmények feldolgozásának grafikus módszere
Az meghatározásához elvileg elegendő az R értékének két különböző hőmérsékleten való ismerete. Azonban az ellenállási értékek különböző párjainak tetszőlegesen választott eredményeiből választva különböző értékeket kapunk .
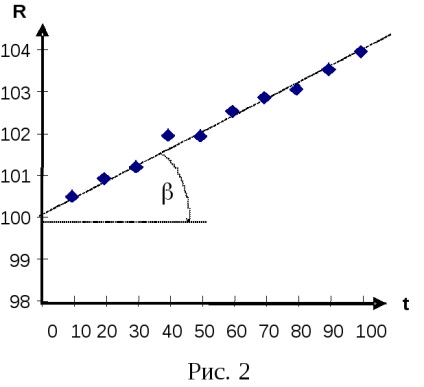
Mivel az R függvénye t-nek lineáris jellegű, a gráfnak egyenesnek kell lennie. Mivel a kísérleti pontok nem egy egyenes vonal mentén húzódnak, olyan grafikonot rajzolunk úgy, hogy a kapott pontok alapvetően egyenletesen helyezkednek el a grafikon mindkét oldalán.
A grafikon metszi az ordinátát egy R0 értéknek megfelelő pontra. azaz ellenállás t = 0 C 0-ban. Az görbéről való megkereséséhez az egyenes meredekségének érintőjét is meg kell határozni. Valójában a (8) képletből:
Amint az a 2. ábrán látható:
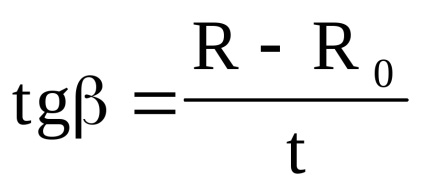
A tan tanuláshoz a legalkalmasabb a (9) képlet alkalmazása, a grafikonba felvett értékek (R-R0) és t értékek helyettesítésével. A kísérlet eredményeinek grafikus ábrázolása lehetővé teszi az egyes mérések pontosságának becslését is. Nyilvánvaló tehát, hogy a grafikon, ahol R = 101,9 Ohm, t = 40 0 C valószínűleg nem kap helyesen, mert a gráf nagyobb távolságra van, mint az R definícióban lévő hármas hiba. Így, amikor egy grafikonot építünk az definíciójában, ezt a pontot el kell dobni.
A rezgés hőmérséklet-együtthatójának meghatározása a grafikon segítségével az egyik kísérleti adatok megoldásának egyik módja. Ugyanakkor meg volt gyõzõdve arról, hogy a kapott adatok nem ellentmondanak a (8) képletnek, bonyolult számítások nélkül találhatják gyorsan megtalálják a rossz eredményt, és kizárják annak hatását a végeredményre.
A grafikon segítségével végzett adatfeldolgozást nagymértékben megkönnyítette, hogy a keresett függőség egyenes vonalú. Nem nehéz egyenes vonalat rajzolni a kísérleti pontokon. És hogyan vezethetünk például a legjobb parabola vagy szinuszodat? Ehhez a grafikon tengelye mentén a skálát kell választani, hogy a várható elméleti függőség egyenes legyen. Tehát például, ha a test gyorsulásával megmérjük a test által t idő alatt áthaladó távolságot, akkor ezeknek a mennyiségeknek a kapcsolatát a következő képlet adja meg:
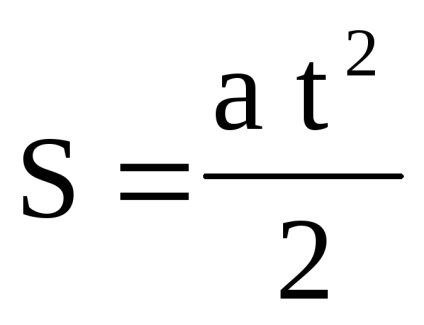
Ha S és t a grafikon tengelyei mentén ábrázoljuk, akkor a kísérleti pontok a parabola közelében találhatók, ami nagyon nehéz szemmel figyelni. Az esetet nagymértékben megkönnyítjük, ha elhalasztjuk az S-t és a t-t a tengelyek mentén vagy t, vagy végül az lnS és az lnt logaritmusainkra. Mindezekben az esetekben a kísérleti pontok egy egyenes vonal közelében helyezkednek el, melyet könnyen szemléltetni kell a megfelelő pontossággal.
Laboratóriumi munka № 1
Téma: "Lineáris mennyiségek mérése"
A "Lineáris mennyiségek mérése" témakör alapvető fontosságú a gyakorlati fizika tanulmányozásához.
Megismerkedem a lineáris mennyiségek mérési módszereivel
Tanuld meg, hogyan használd a mérőcsövet és a mikrométert
Megismerni a kísérleti adatok feldolgozásának módszereit és a mérések pontosságának becslését.
Berendezés: féknyergek, mikrométerek, mért testek.
Terv a téma tanulmányozásához:
A kezdeti tudásszint ellenőrzése.
- egy egyéni szóbeli felmérés, egy elsősoros felmérés.
A téma alapfogalmai és rendelkezései
A Nonius a szokásos skála hozzáadására utal, ami lehetővé teszi a mérés pontosságának 10-20-szoros fokozattal történő növelését.
A lineáris vernier egy kis vonalzó, amely egy nagy vonalzó mellett csúszik, egy skála néven. A vernier oszlopokat általában úgy alkalmazzuk, hogy az egyik vernier osztás (m - 1) / m = 1 - 1 / m része a skálaosztásoknak, ahol m a vernier osztások száma.

Ábra. 1. Lineáris vernier.
Hasonlóképpen nemcsak lineáris, hanem szögletes fogalmakat is felépíthetünk. A vernier féknyeregek féknyergek (2. ábra), teodolitok és sok más eszköz.
A féknyereg (2. ábra) a sávon levő fő osztásokon túlmenően az osztások második skáláját is tartalmazza - a keret belső szélén lévő vernier. Ha a készülék lábszárai szorosan lezárva vannak, mindkét mérleg kezdeti osztódása egybeesik; könnyen láthatjuk, hogy az inius (b) tíz osztása megegyezik az alap skála (a) kilenc osztásával.
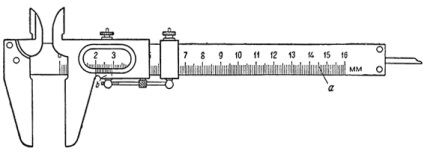
Ábra. 2. Tömlő.
Minden vernierosztás megegyezik a fő skála 0,9 osztásával. Így a fő skála és a vernier osztások közötti különbség az alaprész 0,1 osztása.
Vegyünk egy közelítő mérési eljárást a 3. ábrán látható nagyított vernier modell alkalmazásával.
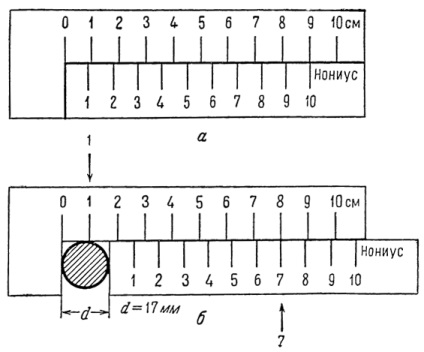
Ábra. 3. A vernier modellje és a mérési folyamat:
a a nulla pozíció; b - mérési terv.
A vernier (3. ábra a) ábrázolása olyan pozícióba, ahol a nulladik osztása egybeesik az alap skála nulla osztásával, könnyen észlelhető 0,1 cm különbség a fő skála minden centiméterén. A vernier minden mozgásával az egyik részleg egybeesik az alap skála egyik részével. A kívánt méret meghatározásához elegendő megnézni, hogy a nónió melyik osztódása egybeesett az alap skálaosztással és sorszámát. Ez megadja a fő skálaosztás tizedének számát. A 3b. Ábra megadja a görgő átmérőjének mérését. Könnyen azt mutatják, hogy az átmérője a értéke között van 1 és 2 cm-es. Mivel a 7 th Division nóniuszos egybeesik az egyik A fő osztályok a skála, ebben az esetben, 8-m, a kívánt mért átmérője d = 1,7 cm.
Microméteres csavar. Mikrométer.
A távolságok pontos mérésére a mikrométeres csavarok - csekély, nagyon pontos és pontosan mért csavarok használatosak. Ilyen csavarokat például precíziós mérőműszerek (mikroszkóp, mikrométer) használnak, és lehetővé teszik akár százmilliárdos mérések elvégzését is. (4. ábra). A mikrométercsavar egy forgatása 0,5 mm-rel mozgatja a rudat. A rúdra csatlakoztatott dob 50 osztásra oszlik. A forgatás egy osztással megegyezik a rúd 0,01 mm-es elmozdulásával. Ezzel a pontossággal a méréseket általában mikrométerrel végezzük. A mikrométercsavar egy pontos rúddal ellátott rúd.
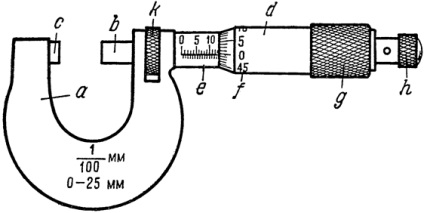
Ábra. 4. Mikrométer. a - a konzol; b - mérőfej; c - sarok; d - egy dobú végtag (kör alakú mérleg); e - szár egy milliméteres skálán; f - végtag, legfeljebb 0,01 mm-es leolvasással; g - hullámos dob; h - racsnis, k - dugó.
A csavar menetének egy fordulatszámban történő emelési magasságát a mikrométer csavar magasságának nevezik. A mikrométer (4. ábra) két fő részből áll: a szorító a és a mikrométer csavar (mérőfej) b. A mikrometrikus csavar belső menettel átjut a konzol lyukaiba, a konzolon lévő mikrometrikus csavarral szemben támasz (vagy sarok) van. A mikrométercsavaron egy teljes henger (dob) van rögzítve a kerület mentén történő osztásokkal. Amikor a mikrométer csavar forog, a dob a vonalán egy lineáris skála mentén csúszik.
Ahhoz, hogy a mikrométercsavar b mozogjon 1 mm-re, a dob két fordulata szükséges. Így a mikrométer csavar magassága 0,5 mm. A dobon lévő mikrométernek van egy skála (végtagja), amely általában 50 rudat tartalmaz. Mivel a csavarmenet szintje s = 0,5 mm, és a bár osztások száma m = 50, a mikrométer pontossága
s / m = 0,5 / 50 = 1/100 mm. (1)
Ennek eredményeképpen a mért tárgy hosszúságának számszerű értéke egy mikrométerrel vagy féknyergekkel van meghatározva
ahol q a skála vonalzójának egésze mm, n a vernier osztás, amely egybeesik a skála vonalzó bármely részével, s / m pedig a pontosság.
Az eredmény lehet a következőkben foglalhatók össze: a minta hosszának, mérve a finombeállító, egyenlő a egész számú körzetek a verniert plusz pontosságot, szorozva az osztás száma a nóniuszos egybeesik egy részlege a skála.