Az előadások matematikája megtalálja a test által a meghatározott felületek által határolt térfogatot
MEGHATÁROZÁS 7. Keresse meg a feltüntetett felület által határolt testet.
Kétféle megoldást kínálunk a testek térfogatának kiszámításához, figyelembe véve a különböző felületi geometriájú testeket.
1). A testet két felület határolja: paraboloid és sík. Húzza ezt a testet a rajzon (75.
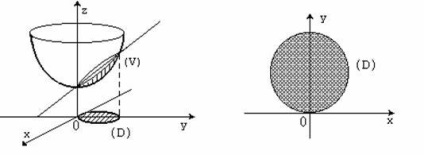
Ez a test egy hengeres gerenda (72. az oldalfelület az adott felületek metszéspontjába degenerálódott. Lássuk azt a régiót, amelyben a testet egy síkra vetítjük ki, amelyre a testhez kötött felületek egyenletéből ki kell zárni a változót (azaz végezzünk ortogonális vetületet):
Így a régió () egy kör, amelynek középpontja a sugár = 1 pontban (0; 1) (lásd a 75. ábrát).
A test térfogatát a hármas integrál segítségével lehet kiszámítani. A Descartes-koordinátarendszerben a hármas integrál a következőképpen íródik át:
amiből kiderül, hogy számítása jelentős nehézségekkel jár (az ismételt integrálszámítás végső szakaszában).
Az integrált egy hengeres koordináta-rendszerben írjuk, amellyel a Descartes-rendszert a képletek kapcsolják össze
Jáciai átalakulás. Az átmeneti képlet (az integrálissá) van formája
A paraboloid és a sík egyenleteit hengeres koordinátarendszerben írjuk:
A körnek van; A szöget természetesen meg kell változtatni 0-ról. Így,
A hengeres rudat a síkra egy görbületes trapéz alakúra (D) vetítjük: 0 # 61603; # 61472; x # 61603; # 61472; 1, 0 # 61603; # 61472; y # 61603; # 61472; . A hármas integrust egy ismételt integrálissá alakítjuk és kiszámítjuk:
Megjegyzés. A hengeres koordináta-rendszerben a számítások egyszerűbbek:
FELVÉTEL 11. Számítsa ki a görbe vonalú integrált részt
a zöld képlet alapján; A zárt kontúr () két görbéből áll: u (lásd a 80. ábrát).
CÍMKE 12. Számítsa ki a görbület () görbületi sűrűségét egy adott sűrűségnél:
1) Figyelembe kell venni a görbe paraméteres specifikációjának () esetét. A síkgörbe tömege kiszámítható az első típusú görbe vonalú integrál segítségével :. Ennek kiszámításához egy változó függvényének egy meghatározott integráljára kell csökkenteni egy intervallumot a következő képlet segítségével:
Az egységtömeg anyagpontjának elmozdulásával kapcsolatos erő kifejtése lineárisan integrálódik az ív mentén pontról pontra
Az utolsó integrál a második alak görbe vonalú integruma az űrgörbe fölött. Számítása egy meghatározott integrál kiszámításához csökken, amelyhez a görbét paraméteres formában kell ábrázolni (a probléma feltétele a kör alakú henger felülete metszéspontjának görbéje, lásd a 81. ábrát).
Egy példa. Lássuk, hol van a sugárvektor modulusa.
Az 5. képlet szerint ez az egyenlőség magában foglalja:
Elértük a radiális függvény sugárirányú funkciójának kiszámítására szolgáló képletet.
Most mérlegeljük a skaláris mező szintfelszínét, azaz az egyenlet által adott felület. Tegyük fel, hogy ez egy folyamatosan differenciálható függvény. Ekkor az érintő sík egyenlete egy olyan ponton, amely ezen a felületen fekszik.
A gradiensvektor koordinátái ennek az egyenletnek együtthatói. Ezért a normális a m-es érintő síkra, és definíció szerint a normál szintre a szint felszínén.
A vektor fluxusa a felületen keresztül. Egy vektor tér eltérése. Legyen egy vektor mező, legyen kétoldalas felület. Legyen az oldal kiválasztása, azaz a normális. Ezt nevezzük a vektor fluxusának a felületen keresztül a megjelölt oldalra.
Ez a kifejezés egybeesik a következő hidrodinamikai problémával. Legyen a folyadékáram sebességének vektora egy időben. Számítsa ki, mennyi folyadék halad át egyszerre egy kis felületen a felületen. Ez a folyadékmennyiség egy henger, amelynek alapja és magassága van, azaz ez a mennyiség egyenlő.
Aztán a teljes felületre megkapjuk. Így az áramlás a folyadékon keresztül folyó mennyiség változása az idő alatt.